The System of Stokes for Fluids
In the case of a flow invariant with respect to the third coordinate (two-dimensional flow), flows at low Reynolds number (for instance micro-organisms) satisfy,
\[\begin{split}\begin{array}{rcl}
-\Delta \mathbf{u} + \nabla p &=& 0\\
\nabla\cdot \mathbf{u} &=& 0
\end{array}\end{split}\]
where \(\mathbf{u}=(u_1,u_2)\) is the fluid velocity and \(p\) its pressure.
The driven cavity is a standard test. It is a box full of liquid with its lid moving horizontally at speed one. The pressure and the velocity must be discretized in compatible fintie element spaces for the LBB conditions to be satisfied:
\[\sup_{p\in P_h}\frac{(\mathbf{u},\nabla p)}{|p|}\geq \beta|\mathbf{u}|~~~\forall \mathbf{u}\in U_h\]
1// Parameters
2int nn = 30;
3
4// Mesh
5mesh Th = square(nn, nn);
6
7// Fespace
8fespace Uh(Th, P1b);
9Uh u, v;
10Uh uu, vv;
11
12fespace Ph(Th, P1);
13Ph p, pp;
14
15// Problem
16solve stokes ([u, v, p], [uu, vv, pp])
17 = int2d(Th)(
18 dx(u)*dx(uu)
19 + dy(u)*dy(uu)
20 + dx(v)*dx(vv)
21 + dy(v)*dy(vv)
22 + dx(p)*uu
23 + dy(p)*vv
24 + pp*(dx(u) + dy(v))
25 - 1e-10*p*pp
26 )
27 + on(1, 2, 4, u=0, v=0)
28 + on(3, u=1, v=0)
29 ;
30
31// Plot
32plot([u, v], p, wait=1);
Note
We add a stabilization term \(\bf{-10e-10*p*pp}\) to fix the constant part of the pressure.
Results are shown on Fig. 21.
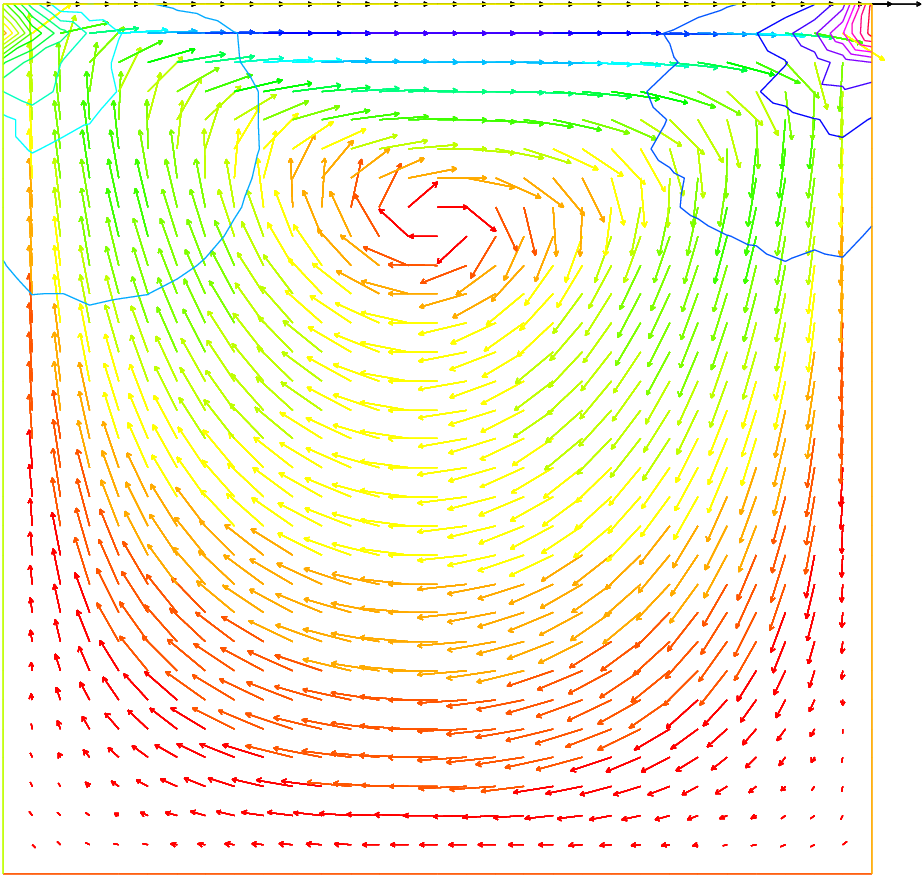
Fig. 21 Solution of Stokes’ equations for the driven cavity problem, showing the velocity field and the pressure level lines.