Newton Method for the Steady Navier-Stokes equations

The problem is find the velocity field \(\mathbf{u}=(u_i)_{i=1}^d\) and the pressure \(p\) of a Flow satisfying in the domain \(\Omega \subset \mathbb{R}^d (d=2,3)\):

\[\begin{split}\begin{array}{rcl} (\mathbf{u}\cdot\nabla) \mathbf{u}-\nu \Delta \mathbf{u}+\nabla p&=&0\\ \nabla\cdot \mathbf{u}&=&0 \end{array}\end{split}\]

where \(\nu\) is the viscosity of the fluid, \(\nabla = (\partial_i )_{i=1}^d\), the dot product is \(\cdot\), and \(\Delta = \nabla\cdot\nabla\) with the same boundary conditions (\(\mathbf{u}\) is given on \(\Gamma\)).

The weak form is find \(\mathbf{u}, p\) such that for \(\forall \mathbf{v}\) (zero on \(\Gamma\)), and \(\forall q\):

\[\int_\Omega ((\mathbf{u}\cdot\nabla) \mathbf{u} ). \mathbf{v} + \nu \nabla \mathbf{u}:\nabla \mathbf{v} - p \nabla\cdot \mathbf{v} - q \nabla\cdot \mathbf{u} = 0\]

The Newton Algorithm to solve nonlinear problem is:

Find \(u\in V\) such that \(F(u)=0\) where \(F : V \mapsto V\).

choose \(u_0\in \mathbb{R}^n\) , ;
for ( \(i =0\); \(i\) < niter; \(i = i+1\))
1. solve \(DF(u_i) w_i = F(u_i)\);
2. \(u_{i+1} = u_i - w_i\);

break \(|| w_i|| < \varepsilon\).

Where \(DF(u)\) is the differential of \(F\) at point \(u\), this is a linear application such that:

\[F(u+\delta) = F(u) + DF(u) \delta + o(\delta)\]

For Navier Stokes, \(F\) and \(DF\) are:

\[\begin{split}\begin{array}{rcl} F(\mathbf{u},p) &=& \int_\Omega((\mathbf{u}\cdot\nabla) \mathbf{u} ). \mathbf{v} + \nu \nabla \mathbf{u}:\nabla \mathbf{v} - p \nabla\cdot \mathbf{v} - q \nabla\cdot \mathbf{u}\\ DF(\mathbf{u},p)(\mathbf{\delta u} ,\delta p) &=& \int_\Omega ((\mathbf{\delta u}\cdot\nabla) \mathbf{u} ). \mathbf v + ((\mathbf{u}\cdot\nabla) \mathbf{\delta u} ). \mathbf{v} \\ &+& \nu \nabla \mathbf{\delta u}:\nabla \mathbf{v} - \delta p \nabla\cdot \mathbf{v} - q \nabla\cdot \mathbf{\delta u} \end{array}\end{split}\]

So the Newton algorithm become:

// Parameters
real R = 5.;
real L = 15.;

real nu = 1./50.;
real nufinal = 1/200.;
real cnu = 0.5;

real eps = 1e-6;

verbosity = 0;

// Mesh
border cc(t=0, 2*pi){x=cos(t)/2.; y=sin(t)/2.; label=1;}
border ce(t=pi/2, 3*pi/2){x=cos(t)*R; y=sin(t)*R; label=1;}
border beb(tt=0, 1){real t=tt^1.2; x=t*L; y=-R; label=1;}
border beu(tt=1, 0){real t=tt^1.2; x=t*L; y=R; label=1;}
border beo(t=-R, R){x=L; y=t; label=0;}
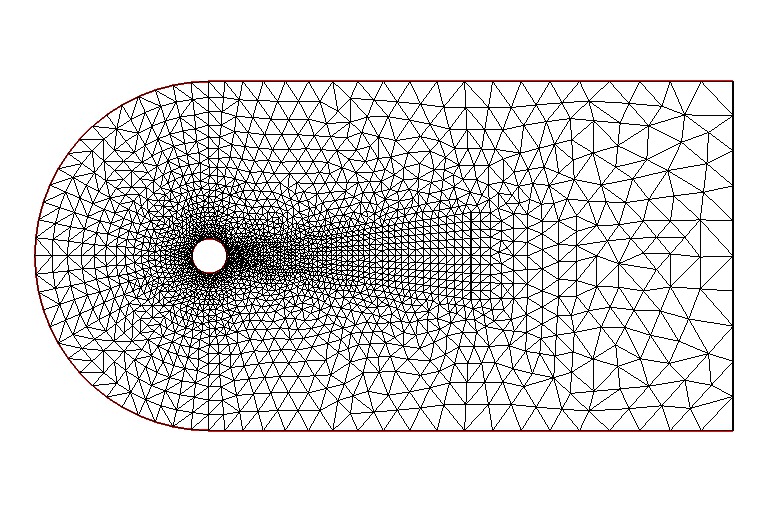
border bei(t=-R/4, R/4){x=L/2; y=t; label=0;}
mesh Th = buildmesh(cc(-50) + ce(30) + beb(20) + beu(20) + beo(10) + bei(10));
plot(Th);

//bounding box for the plot
func bb = [[-1,-2],[4,2]];

// Fespace
fespace Xh(Th, P2);
Xh u1, u2;
Xh v1,v2;
Xh du1,du2;
Xh u1p,u2p;

fespace Mh(Th,P1);
Mh p;
Mh q;
Mh dp;
Mh pp;

// Macro
macro Grad(u1,u2) [dx(u1), dy(u1), dx(u2),dy(u2)] //
macro UgradV(u1,u2,v1,v2) [[u1,u2]'*[dx(v1),dy(v1)],
                        [u1,u2]'*[dx(v2),dy(v2)]] //
macro div(u1,u2) (dx(u1) + dy(u2)) //

// Initialization
u1 = (x^2+y^2) > 2;
u2 = 0;

// Viscosity loop
while(1){
    int n;
    real err=0;
    // Newton loop
    for (n = 0; n < 15; n++){
        // Newton
        solve Oseen ([du1, du2, dp], [v1, v2, q])
            = int2d(Th)(
                    nu * (Grad(du1,du2)' * Grad(v1,v2))
                + UgradV(du1,du2, u1, u2)' * [v1,v2]
                + UgradV( u1, u2,du1,du2)' * [v1,v2]
                - div(du1,du2) * q
                - div(v1,v2) * dp
                - 1e-8*dp*q //stabilization term
            )
            - int2d(Th) (
                    nu * (Grad(u1,u2)' * Grad(v1,v2))
                + UgradV(u1,u2, u1, u2)' * [v1,v2]
                - div(u1,u2) * q
                - div(v1,v2) * p
            )
            + on(1, du1=0, du2=0)
            ;

        u1[] -= du1[];
        u2[] -= du2[];
        p[] -= dp[];

        real Lu1=u1[].linfty, Lu2=u2[].linfty, Lp=p[].linfty;
        err = du1[].linfty/Lu1 + du2[].linfty/Lu2 + dp[].linfty/Lp;

        cout << n << " err = " << err << " " << eps << " rey = " << 1./nu << endl;
        if(err < eps) break; //converge
        if( n>3 && err > 10.) break; //blowup
    }

    if(err < eps){  //converge: decrease $\nu$ (more difficult)
        // Plot
        plot([u1, u2], p, wait=1, cmm=" rey = " + 1./nu , coef=0.3, bb=bb);

        // Change nu
        if( nu == nufinal) break;
        if( n < 4) cnu = cnu^1.5; //fast converge => change faster
        nu = max(nufinal, nu* cnu); //new viscosity

        // Update
        u1p = u1;
        u2p = u2;
        pp = p;
    }
    else{   //blowup: increase $\nu$ (more simple)
        assert(cnu< 0.95); //the method finally blowup

        // Recover nu
        nu = nu/cnu;
        cnu= cnu^(1./1.5); //no conv. => change lower
        nu = nu* cnu; //new viscosity
        cout << " restart nu = " << nu << " Rey = " << 1./nu << " (cnu = " << cnu << " ) \n";

        // Recover a correct solution
        u1 = u1p;
        u2 = u2p;
        p = pp;
    }
}

Note

We use a trick to make continuation on the viscosity \(\nu\), because the Newton method blowup owe start with the final viscosity \(\nu\).

\(\nu\) is gradually increased to the desired value.

NSNewtonUP — Fig. 26 Velocity and pressure

Naver-Stokes newton