FreeFEM Documentation on GitHub

stars - forks

Transmission problem

Consider an elastic plate whose displacement change vertically, which is made up of three plates of different materials, welded on each other.

Let \(\Omega_i\), \(i=1,2,3\) be the domain occupied by \(i\)-th material with tension \(\mu_i\) (see Soap film).

The computational domain \(\Omega\) is the interior of \(\overline{\Omega_1}\cup \overline{\Omega_2}\cup \overline{\Omega_3}\). The vertical displacement \(u(x,y)\) is obtained from:

(72)\[\begin{split}\begin{array}{rcll} -\mu_i\Delta u &=& f & \textrm{ in }\Omega_i\\ \mu_i\p_n u|_{\Gamma_{i}} &=& -\mu_j\p_n u|_{\Gamma_{j}} & \textrm{ on }\overline{\Omega_{i}}\cap\overline{\Omega_{j}} \textrm{ if }1\le i< j\le 3 \end{array}\end{split}\]

where \(\p_n u|_{\Gamma_{i}}\) denotes the value of the normal derivative \(\p_n u\) on the boundary \(\Gamma_i\) of the domain \(\Omega_i\).

By introducing the characteristic function \(\chi_i\) of \(\Omega_i\), that is:

\[\chi_i(x)=1\ \textrm{ if }x\in\Omega_i;\ \chi_i(x)=0\ \textrm{ if }x\not\in\Omega_i\]

we can easily rewrite (72) to the weak form. Here we assume that \(u=0\) on \(\Gamma=\p\Omega\).

Transmission problem: For a given function \(f\), find \(u\) such that:

\[a(u,v) = \ell(f,v) \textrm{ for all }v\in H^1_0(\Omega)\]
\[\begin{split}\begin{array}{rcl} a(u,v) &=& \int_{\Omega}\mu \nabla u\cdot \nabla v\nonumber\\ \ell(f,v) &=& \int_{\Omega}fv\nonumber \end{array}\end{split}\]

where \(\mu=\mu_1\chi_1+\mu_2\chi_2+\mu_3\chi_3\). Here we notice that \(\mu\) become the discontinuous function.

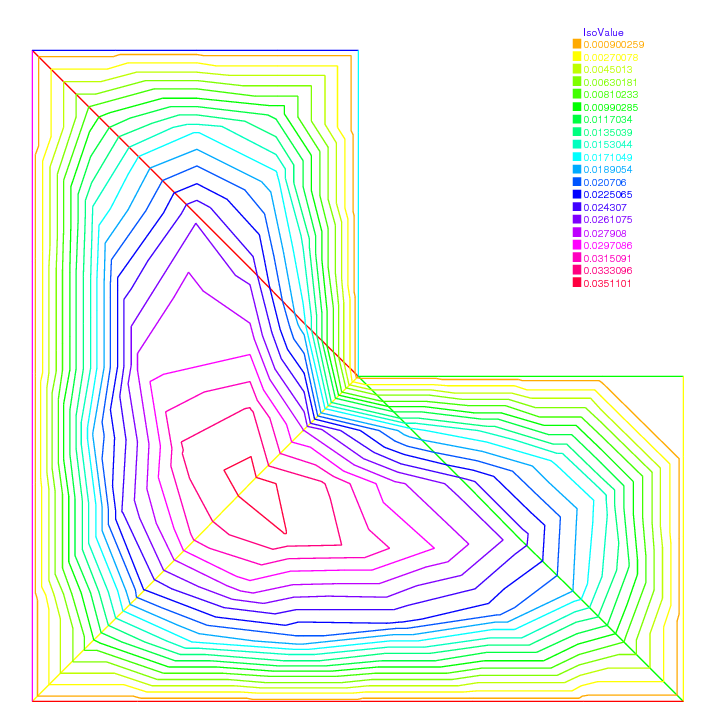
This example explains the definition and manipulation of region, i.e. sub-domains of the whole domain. Consider this L-shaped domain with 3 diagonals as internal boundaries, defining 4 sub-domains:

 1// Mesh
 2border a(t=0, 1){x=t; y=0;};
 3border b(t=0, 0.5){x=1; y=t;};
 4border c(t=0, 0.5){x=1-t; y=0.5;};
 5border d(t=0.5, 1){x=0.5; y=t;};
 6border e(t=0.5, 1){x=1-t; y=1;};
 7border f(t=0, 1){x=0; y=1-t;};
 8border i1(t=0, 0.5){x=t; y=1-t;};
 9border i2(t=0, 0.5){x=t; y=t;};
10border i3(t=0, 0.5){x=1-t; y=t;};
11mesh th = buildmesh(a(6) + b(4) + c(4) +d(4) + e(4)
12    + f(6) + i1(6) + i2(6) + i3(6));
13
14// Fespace
15fespace Ph(th, P0); //constant discontinuous functions / element
16Ph reg=region; //defined the P0 function associated to region number
17
18// Plot
19plot(reg, fill=true, wait=true, value=true);
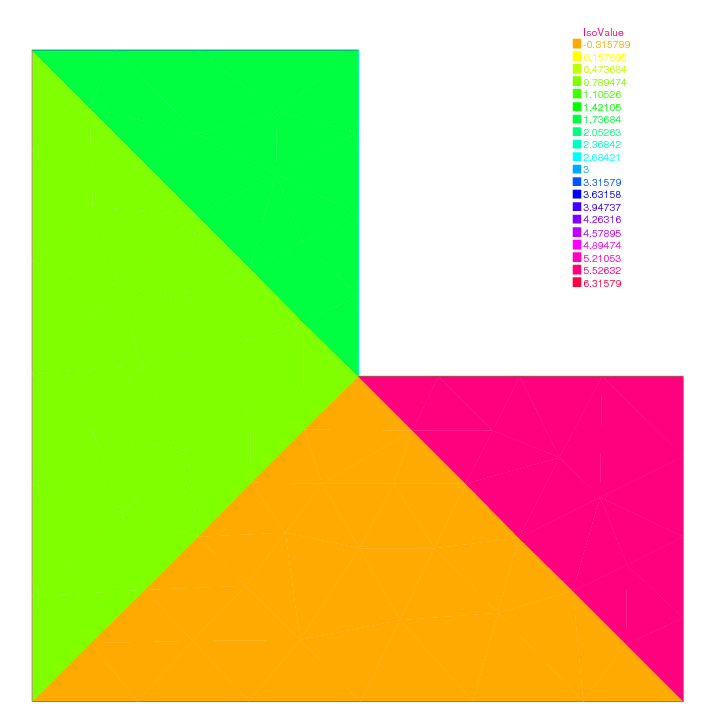
TransmissionProblem_Region

Fig. 176 The function reg

region is a keyword of FreeFEM which is in fact a variable depending of the current position (is not a function today, use Ph reg=region; to set a function). This variable value returned is the number of the sub-domain of the current position. This number is defined by buildmesh which scans while building the mesh all its connected component.

So to get the number of a region containing a particular point one does:

1// Characteristic function
2int nupper = reg(0.4, 0.9); //get the region number of point (0.4,0.9)
3int nlower = reg(0.9, 0.1); //get the region number of point (0.4,0.1)
4cout << "nlower = " <<  nlower << ", nupper = " << nupper<< endl;
5Ph nu = 1 + 5*(region==nlower) + 10*(region==nupper);
6
7// Plot
8plot(nu, fill=true,wait=true);
TransmissionProblem_Nu

Fig. 177 The function nu

This is particularly useful to define discontinuous functions such as might occur when one part of the domain is copper and the other one is iron, for example.

We this in mind we proceed to solve a Laplace equation with discontinuous coefficients (\(\nu\) is 1, 6 and 11 below).

 1// Problem
 2solve lap (u, v)
 3    = int2d(th)(
 4          nu*(dx(u)*dx(v) + dy(u)*dy(v))
 5    )
 6    + int2d(th)(
 7        - 1*v
 8    )
 9    + on(a, b, c, d, e, f, u=0)
10    ;
11
12// Plot
13plot(u);
TransmissionProblem_U

Fig. 178 The isovalue of the solution \(u\)

Table of content