Non-linear elasticity

The nonlinear elasticity problem is: find the displacement \((u_{1},u_{2})\) minimizing \(J\):

\[\min J(u_{1},u_{2}) = \int_{\Omega} f(F2) - \int_{\Gamma_{p}} P_{a} \, u_{2}\]

where \(F2(u_{1},u_{2}) = A(E[u_{1},u_{2}],E[u_{1},u_{2}])\) and \(A(X,Y)\) is bilinear symmetric positive form with respect two matrix \(X,Y\).

where \(f\) is a given \(\mathcal{C}^2\) function, and \(E[u_{1},u_{2}] = (E_{ij})_{i=1,2,\,j=1,2}\) is the Green-Saint Venant deformation tensor defined with:

\[E_{ij} = 0.5 \big( ( \p_i u_j + \p_j u_i ) + \sum_k \p_i u_k {\times} \p_j u_k \big)\]

Denote \(\mathbf{u}=(u_{1},u_{2})\), \(\mathbf{v}=(v_{1},v_{2})\), \(\mathbf{w}=(w_{1},w_{2})\). So, the differential of \(J\) is:

\[DJ(\mathbf{u})(\mathbf{v}) = \int DF2(\mathbf{u})(\mathbf{v}) \;f'(F2(\mathbf{u}))) - \int_{\Gamma_{p}} P_{a} v_{2}\]

where \(DF2(\mathbf{u})(\mathbf{v}) = 2 \; A(DE[\mathbf{u}](\mathbf{v}),E[\mathbf{u}])\) and \(DE\) is the first differential of \(E\).

The second order differential is:

\[\begin{split}\begin{array}{rcl} D^2 J(\mathbf{u})((\mathbf{v}),(\mathbf{w})) &=& \displaystyle\int DF2(\mathbf{u})(\mathbf{v}) \; DF2(\mathbf{u})(\mathbf{w}) \; f''(F2(\mathbf{u}))) \\ &+& \displaystyle\int \; D^2F2(\mathbf{u})(\mathbf{v},\mathbf{w}) \; f'(F2(\mathbf{u}))) \end{array}\end{split}\]

where:

\[D^2F2(\mathbf{u})(\mathbf{v},\mathbf{w}) = 2 \; A(\;D^2E[\mathbf{u}](\mathbf{v},\mathbf{w})\;,\;E[\mathbf{u}]\;) + 2 \; A(\;DE[\mathbf{u}](\mathbf{v})\;,DE[\mathbf{u}](\mathbf{w})\;) .\]

and \(D^{2}E\) is the second differential of \(E\).

So all notations can be define with macro:

 macro EL(u, v) [dx(u), (dx(v)+dy(u)), dy(v)] //is [epsilon_11, 2epsilon_12, epsilon_22]

 macro ENL(u, v) [
     (dx(u)*dx(u) + dx(v)*dx(v))*0.5,
     (dx(u)*dy(u) + dx(v)*dy(v)),
     (dy(u)*dy(u) + dy(v)*dy(v))*0.5
 ] //

 macro dENL(u, v, uu, vv) [
     (dx(u)*dx(uu) + dx(v)*dx(vv)),
     (dx(u)*dy(uu) + dx(v)*dy(vv) + dx(uu)*dy(u) + dx(vv)*dy(v)),
     (dy(u)*dy(uu) + dy(v)*dy(vv))
 ] //

 macro E(u, v) (EL(u,v) + ENL(u,v)) //is [E_11, 2E_12, E_22]
 macro dE(u, v, uu, vv) (EL(uu, vv) + dENL(u, v, uu, vv)) //
 macro ddE(u, v, uu, vv, uuu, vvv) dENL(uuu, vvv, uu, vv) //
 macro F2(u, v) (E(u, v)'*A*E(u, v)) //
 macro dF2(u, v, uu, vv) (E(u, v)'*A*dE(u, v, uu, vv)*2.) //
 macro ddF2(u, v, uu, vv, uuu, vvv) (
     (dE(u, v, uu, vv)'*A*dE(u, v, uuu, vvv))*2.
     + (E(u, v)'*A*ddE(u, v, uu, vv, uuu, vvv))*2.
 ) //

The Newton Method is:

choose \(n=0\),and \(u_0,v_0\) the initial displacement

loop:
- find \((du,dv)\) : solution of
  
  \[D^2J(u_n,v_n)((w,s),(du,dv)) = DJ(u_n,v_n)(w,s) , \quad \forall w,s\]
- \(un = un - du,\quad vn =vn - dv\)
- until \((du,dv)\) small is enough

The way to implement this algorithm in FreeFEM is use a macro tool to implement \(A\) and \(F2\), \(f\), \(f'\),\(f''\).

A macro is like in ccp preprocessor of C++, but this begin by macro and the end of the macro definition is before the comment //. In this case the macro is very useful because the type of parameter can be change. And it is easy to make automatic differentiation.

../_images/NonLinearElasticity_Mesh1.png — Fig. 182 The deformed domain

// Macro
macro EL(u, v) [dx(u), (dx(v)+dy(u)), dy(v)] //is [epsilon_11, 2epsilon_12, epsilon_22]

macro ENL(u, v) [
    (dx(u)*dx(u) + dx(v)*dx(v))*0.5,
    (dx(u)*dy(u) + dx(v)*dy(v)),
    (dy(u)*dy(u) + dy(v)*dy(v))*0.5
    ] //

macro dENL(u, v, uu, vv) [
    (dx(u)*dx(uu) + dx(v)*dx(vv)),
    (dx(u)*dy(uu) + dx(v)*dy(vv) + dx(uu)*dy(u) + dx(vv)*dy(v)),
    (dy(u)*dy(uu) + dy(v)*dy(vv))
    ] //

macro E(u, v) (EL(u,v) + ENL(u,v)) //is [E_11, 2E_12, E_22]
macro dE(u, v, uu, vv) (EL(uu, vv) + dENL(u, v, uu, vv)) //
macro ddE(u, v, uu, vv, uuu, vvv) dENL(uuu, vvv, uu, vv) //
macro F2(u, v) (E(u, v)'*A*E(u, v)) //
macro dF2(u, v, uu, vv) (E(u, v)'*A*dE(u, v, uu, vv)*2.) //
macro ddF2(u, v, uu, vv, uuu, vvv) (
      (dE(u, v, uu, vv)'*A*dE(u, v, uuu, vvv))*2.
    + (E(u, v)'*A*ddE(u, v, uu, vv, uuu, vvv))*2.
    ) //

macro f(u) ((u)*(u)*0.25) //
macro df(u) ((u)*0.5) //
macro ddf(u) (0.5) //

// Parameters
real mu = 0.012e5; //kg/cm^2
real lambda = 0.4e5; //kg/cm^2
real Pa = 1e2;

// sigma = 2 mu E + lambda tr(E) Id
// A(u,v) = sigma(u):E(v)
//
// ( a b )
// ( b c )
//
// tr*Id : (a,b,c) -> (a+c,0,a+c)
// so the associed matrix is:
// ( 1 0 1 )
// ( 0 0 0 )
// ( 1 0 1 )

real a11 = 2*mu + lambda;
real a22 = mu; //because [0, 2*t12, 0]' A [0, 2*s12,0] = 2*mu*(t12*s12 + t21*s21) = 4*mu*t12*s12
real a33 = 2*mu + lambda;
real a12 = 0;
real a13 = lambda;
real a23 = 0;
// symetric part
real a21 = a12;
real a31 = a13;
real a32 = a23;

//the matrix A
func A = [[a11, a12, a13], [a21, a22, a23], [a31, a32, a33]];

// Mesh
int n = 30;
int m = 10;
mesh Th = square(n, m, [x, .3*y]); //label: 1 bottom, 2 right, 3 up, 4 left;
int bottom = 1, right = 2, upper = 3, left = 4;
plot(Th);

// Fespace
fespace Wh(Th, P1dc);
Wh e2, fe2, dfe2, ddfe2;

fespace Vh(Th, [P1, P1]);
Vh [uu, vv] = [0, 0], [w, s], [un, vn] = [0, 0];

fespace Sh(Th, P1);
Sh u1, v1;

// Problem
varf vmass ([uu, vv], [w, s], solver=CG) = int2d(Th)(uu*w + vv*s);
matrix M = vmass(Vh, Vh);
problem NonLin([uu, vv], [w, s], solver=LU)
    = int2d(Th, qforder=1)( //(D^2 J(un))
           dF2(un, vn, uu, vv)*dF2(un, vn, w, s)*ddfe2
        + ddF2(un, vn, uu, vv, w, s)*ddfe2
    )
    - int1d(Th, upper)(
          Pa*s
    )
    - int2d(Th, qforder=1)( //(D J(un))
          dF2(un, vn, w, s)*dfe2
    )
    + on(right, left, uu=0, vv=0)
    ;

// Newton's method
for (int i = 0; i < 10; i++){
    cout << "Loop " << i << endl;

    // Update
    e2 = F2(un, vn);
    dfe2 = df(e2) ;
    ddfe2 = ddf(e2);
    cout << "e2 max = " <<e2[].max << ", min = " << e2[].min << endl;
    cout << "de2 max = "<< dfe2[].max << ", min = " << dfe2[].min << endl;
    cout << "dde2 max = "<< ddfe2[].max << ", min = " << ddfe2[].min << endl;

    // Solve
    NonLin;
    w[]  = M*uu[];

    // Residual
    real res = sqrt(w[]' * uu[]); //L^2 norm of [uu, vv]
    cout << " L^2 residual = " << res << endl;

    // Update
    v1 = vv;
    u1 = uu;
    cout << "u1 min = " <<u1[].min << ", u1 max = " << u1[].max << endl;
    cout << "v1 min = " <<v1[].min << ", v2 max = " << v1[].max << endl;

    // Plot
    plot([uu, vv], wait=true, cmm="uu, vv");

    // Update
    un[] -= uu[];
    plot([un, vn], wait=true, cmm="displacement");

    if (res < 1e-5) break;
}

// Plot
plot([un, vn], wait=true);

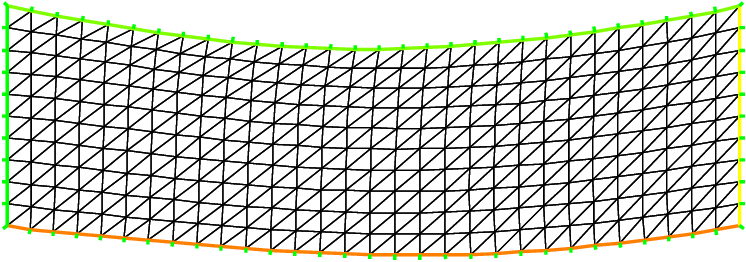
// Movemesh
mesh th1 = movemesh(Th, [x+un, y+vn]);

// Plot
plot(th1, wait=true);

Here you can use the search bar to search in all FreeFEM examples instead

The list of all matching examples on the right is updated for each new query

Clicking on a search hit or on an example on the right brings up the corresponding script from GitHub

You can also filter the list on the right by selecting one or more intersecting categories on the left tree

Non-linear elasticity