Visualization
Plot
1mesh Th = square(5,5);
2fespace Vh(Th, P1);
3
4// Plot scalar and vectorial FE function
5Vh uh=x*x+y*y, vh=-y^2+x^2;
6plot(Th, uh, [uh, vh], value=true, wait=true);
7
8// Zoom on box defined by the two corner points [0.1,0.2] and [0.5,0.6]
9plot(uh, [uh, vh], bb=[[0.1, 0.2], [0.5, 0.6]],
10 wait=true, grey=true, fill=true, value=true);
11
12// Compute a cut
13int n = 10;
14real[int] xx(10), yy(10);
15for (int i = 0; i < n; i++){
16 x = i/real(n);
17 y = i/real(n);
18 xx[i] = i;
19 yy[i] = uh; // Value of uh at point (i/10., i/10.)
20}
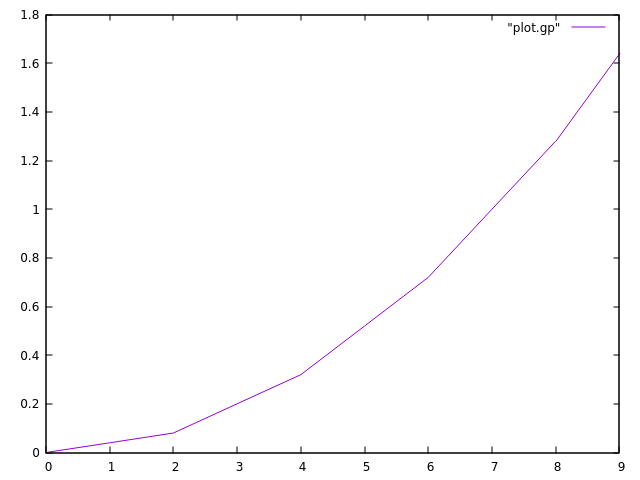
21plot([xx, yy], wait=true);
22
23{ // File for gnuplot
24 ofstream gnu("plot.gp");
25 for (int i = 0; i < n; i++)
26 gnu << xx[i] << " " << yy[i] << endl;
27}
28
29// Calls the gnuplot command, waits 5 seconds and generates a postscript plot (UNIX ONLY)
30exec("echo 'plot \"plot.gp\" w l \n pause 5 \n set term postscript \n set output \"gnuplot.eps\" \n replot \n quit' | gnuplot");
HSV
1// From: http://en.wikipedia.org/wiki/HSV_color_space
2// The HSV (Hue, Saturation, Value) model defines a color space
3// in terms of three constituent components:
4// HSV color space as a color wheel
5// Hue, the color type (such as red, blue, or yellow):
6// Ranges from 0-360 (but normalized to 0-100% in some applications like here)
7// Saturation, the "vibrancy" of the color: Ranges from 0-100%
8// The lower the saturation of a color, the more "grayness" is present
9// and the more faded the color will appear.
10// Value, the brightness of the color: Ranges from 0-100%
11
12mesh Th = square(10, 10, [2*x-1, 2*y-1]);
13
14fespace Vh(Th, P1);
15Vh uh=2-x*x-y*y;
16
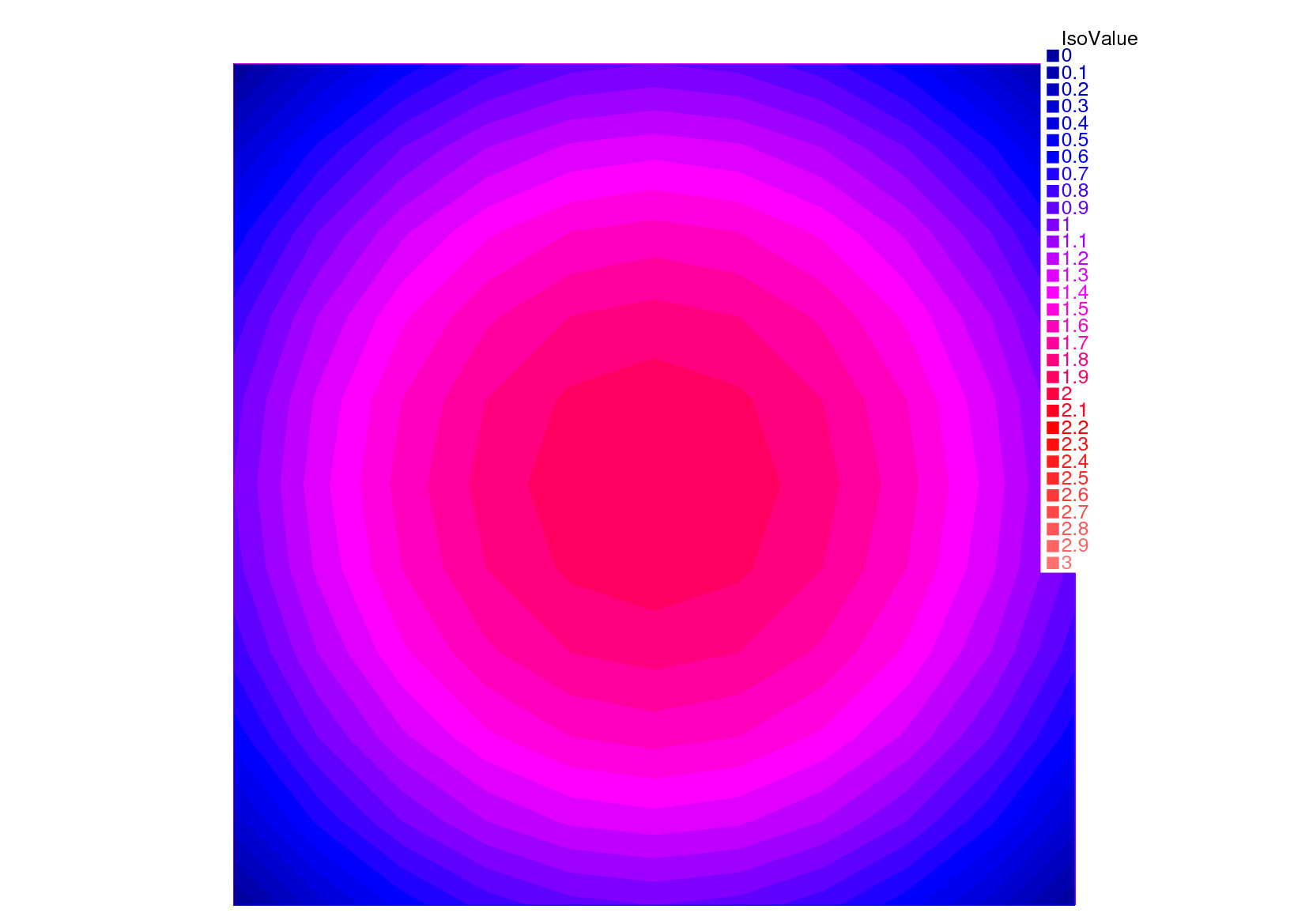
17real[int] colorhsv=[ // Color hsv model
18 4./6., 1 , 0.5, // Dark blue
19 4./6., 1 , 1, // Blue
20 5./6., 1 , 1, // Magenta
21 1, 1. , 1, // Red
22 1, 0.5 , 1 // Light red
23 ];
24 real[int] viso(31);
25
26 for (int i = 0; i < viso.n; i++)
27 viso[i] = i*0.1;
28
29 plot(uh, viso=viso(0:viso.n-1), value=true, fill=true, wait=true, hsv=colorhsv);
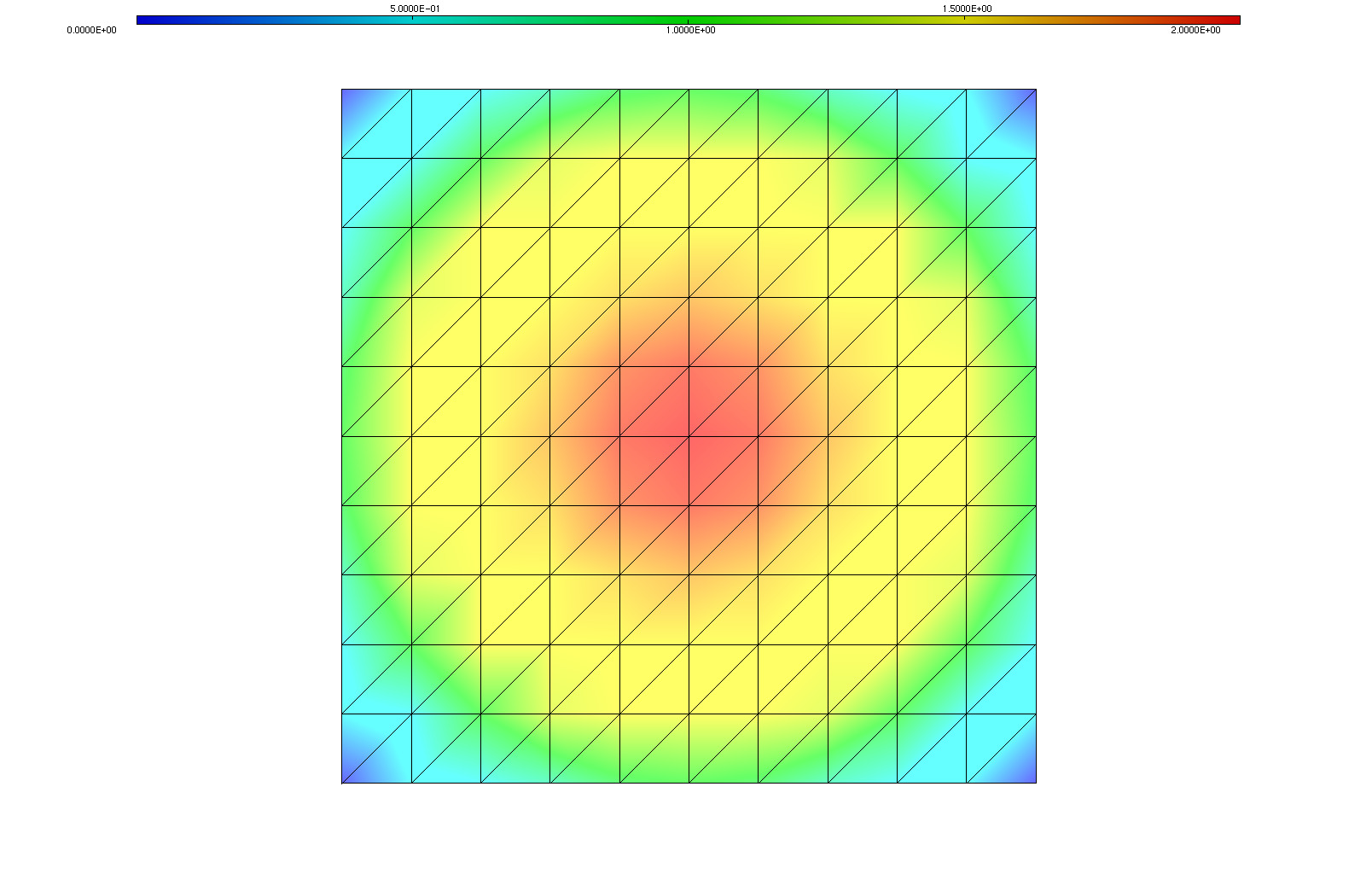
Medit
1load "medit"
2
3mesh Th = square(10, 10, [2*x-1, 2*y-1]);
4
5fespace Vh(Th, P1);
6Vh u=2-x*x-y*y;
7
8medit("u", Th, u);
9
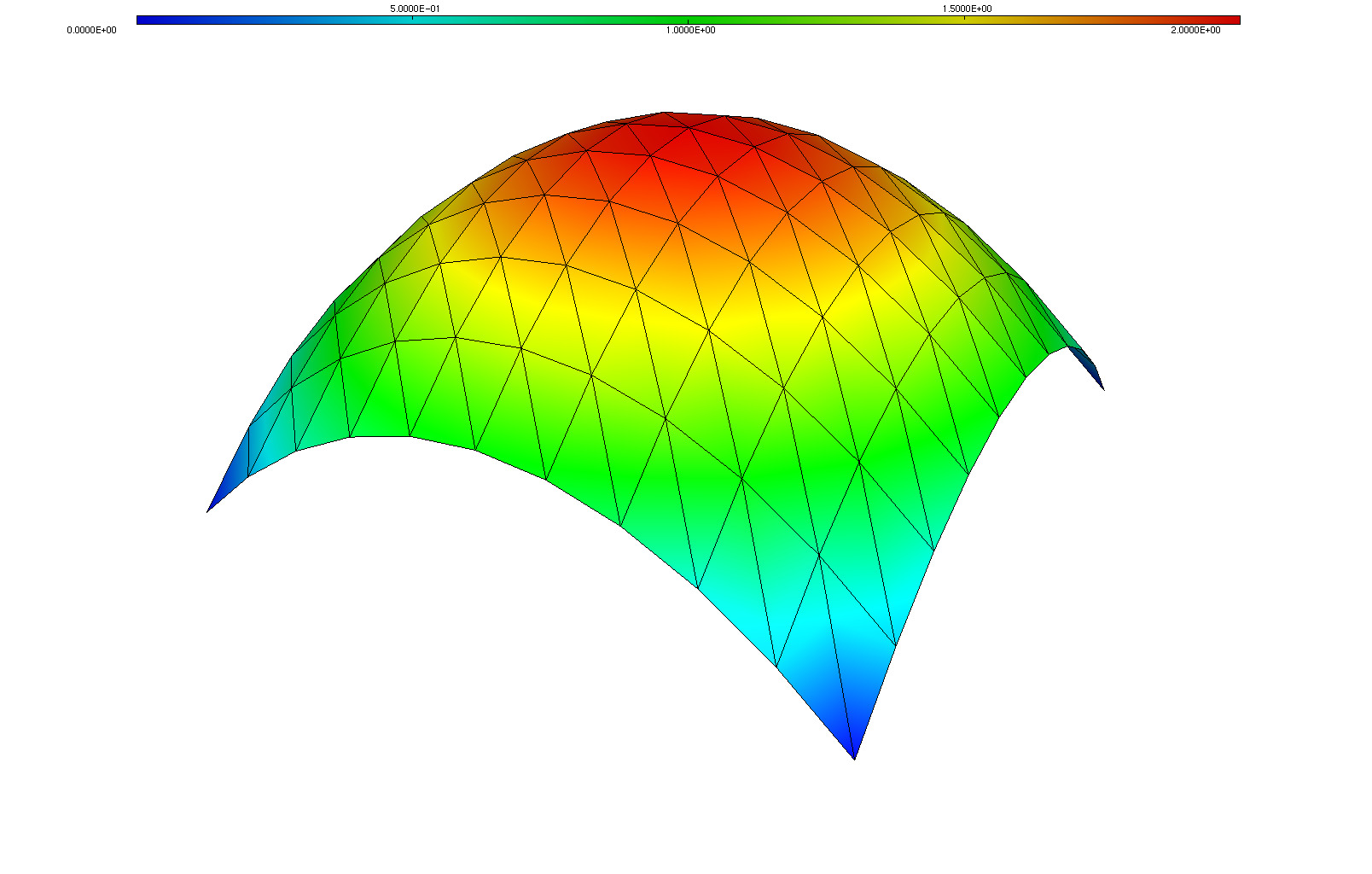
10// Old way
11savemesh(Th, "u", [x, y, u*.5]); // Saves u.points and u.faces file
12// build a u.bb file for medit
13{
14 ofstream file("u.bb");
15 file << "2 1 1 " << u[].n << " 2 \n";
16 for (int j = 0; j < u[].n; j++)
17 file << u[][j] << endl;
18}
19// Calls medit command
20exec("ffmedit u");
21// Cleans files on unix-like OS
22exec("rm u.bb u.faces u.points");
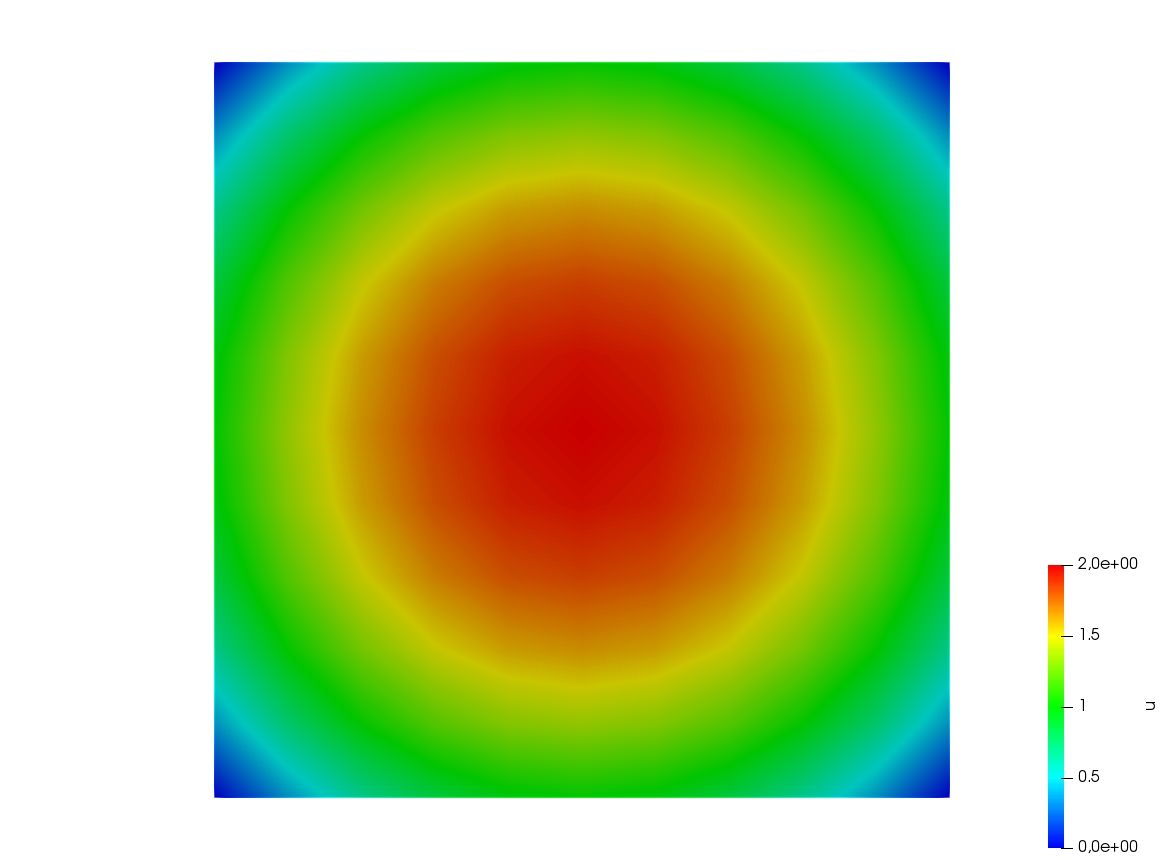
Paraview
1load "iovtk"
2
3mesh Th = square(10, 10, [2*x-1, 2*y-1]);
4
5fespace Vh(Th, P1);
6Vh u=2-x*x-y*y;
7
8int[int] Order = [1];
9string DataName = "u";
10savevtk("u.vtu", Th, u, dataname=DataName, order=Order);