Developers

FFT

load "dfft"

// Parameters
int nx = 32;
real ny = 16;
real N = nx*ny;
func f1 = cos(2*x*2*pi)*cos(3*y*2*pi);

// Mesh
//warning: the fourier space is not exactly the unit square due to periodic condition
mesh Th = square(nx-1, ny-1, [(nx-1)*x/nx, (ny-1)*y/ny]);
//warning: the numbering of the vertices (x,y) is
//given by i = x/nx + nx*y/ny

// Fespace
fespace Vh(Th,P1);
Vh<complex> u = f1, v;
Vh w = f1;
Vh ur, ui;

// FFT
//in dfft the matrix n, m is in row-major order and array n, m is
//store j + m*i (the transpose of the square numbering)
v[] = dfft(u[], ny, -1);
u[] = dfft(v[], ny, +1);
cout << "||u||_\infty " << u[].linfty << endl;

u[] *= 1./N;
cout << "||u||_\infty " << u[].linfty << endl;

ur = real(u);

// Plot
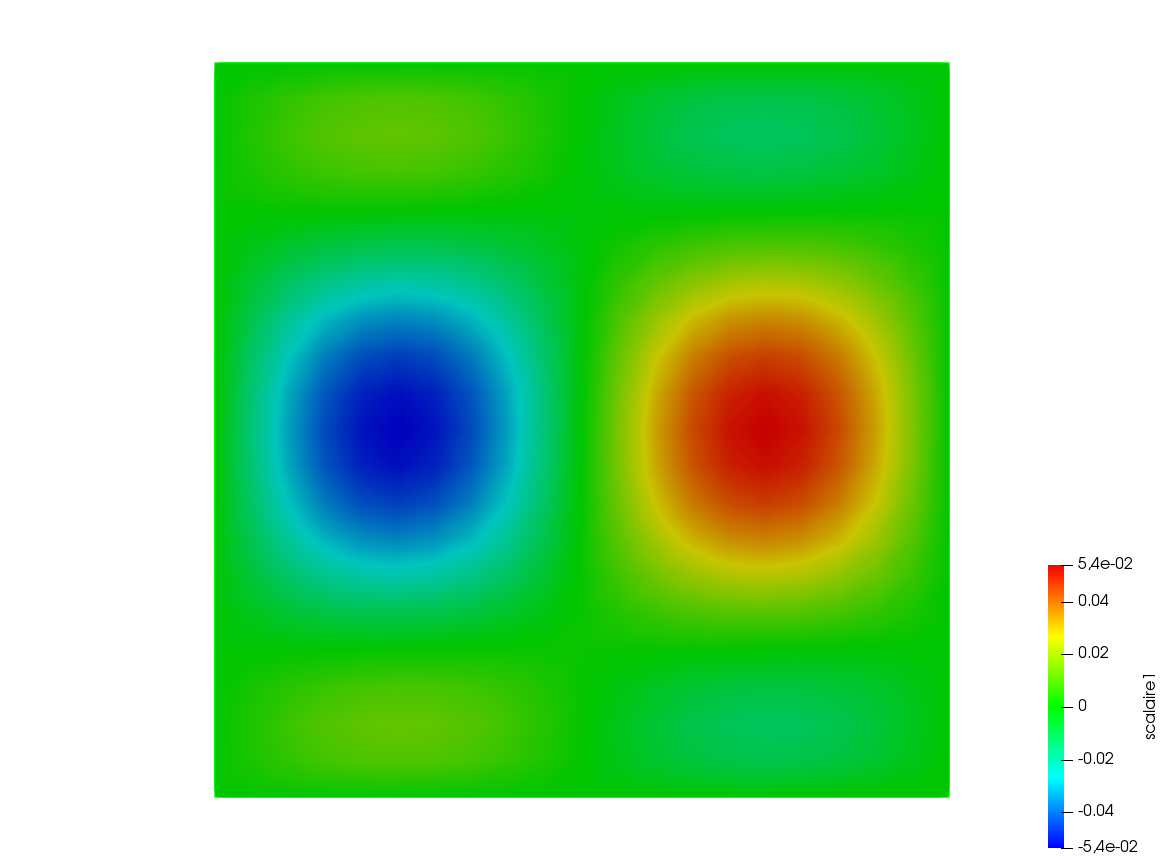
plot(w, wait=1, value=1, cmm="w");
plot(ur, wait=1, value=1, cmm="u");
v = w - u;
cout << "diff = " << v[].max << " " << v[].min << endl;
assert( norm(v[].max) < 1e-10 && norm(v[].min) < 1e-10);

// Other example
//FFT Lapacian
//-\Delta u = f with biperiodic condition
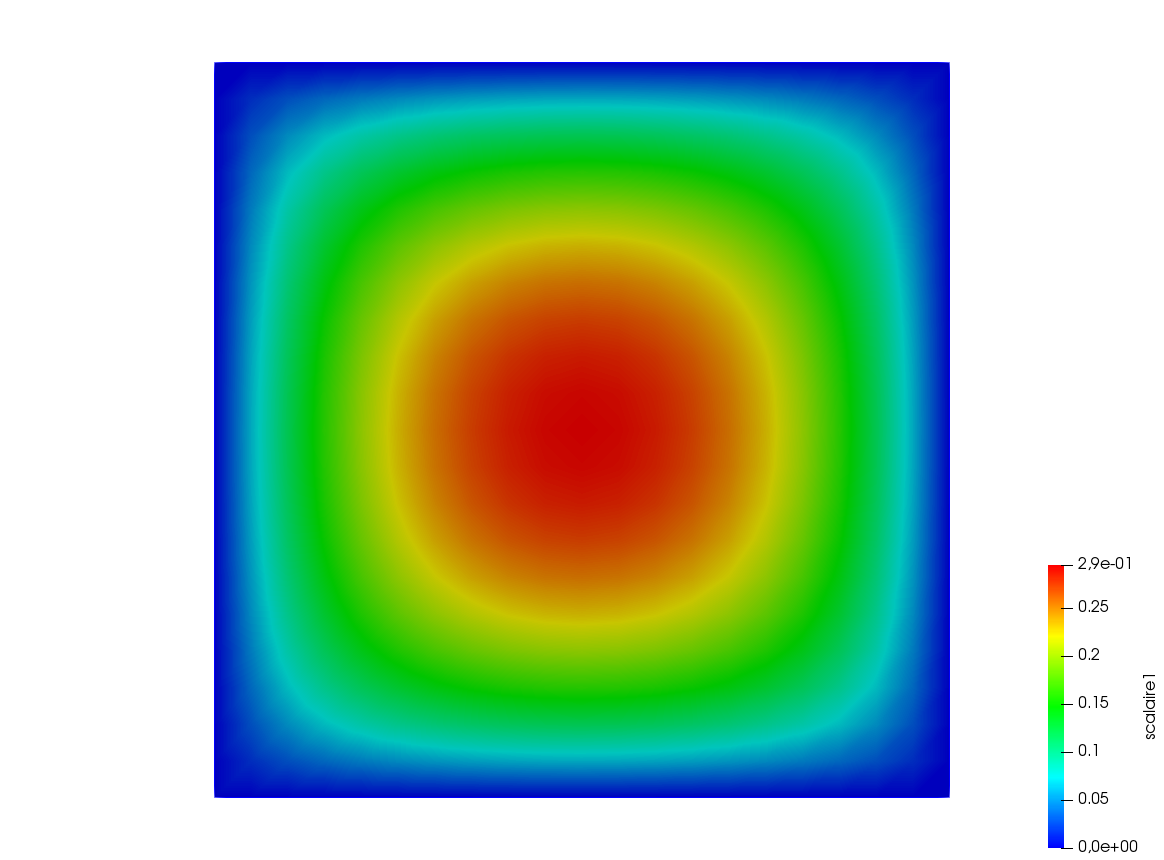
func f = cos(3*2*pi*x)*cos(2*2*pi*y);
func ue = (1./(square(2*pi)*13.))*cos(3*2*pi*x)*cos(2*2*pi*y); //the exact solution
Vh<complex> ff = f;
Vh<complex> fhat;
Vh<complex> wij;

// FFT
fhat[] = dfft(ff[],ny,-1);

//warning in fact we take mode between -nx/2, nx/2 and -ny/2, ny/2
//thanks to the operator ?:
wij = square(2.*pi)*(square(( x<0.5?x*nx:(x-1)*nx)) + square((y<0.5?y*ny:(y-1)*ny)));
wij[][0] = 1e-5; //to remove div / 0
fhat[] = fhat[] ./ wij[];
u[] = dfft(fhat[], ny, 1);
u[] /= complex(N);
ur = real(u); //the solution
w = real(ue); //the exact solution

// Plot
plot(w, ur, value=1, cmm="ue", wait=1);

// Error
w[] -= ur[];
real err = abs(w[].max) + abs(w[].min);
cout << "err = " << err << endl;
assert(err < 1e-6);

fftwplan p1 = plandfft(u[], v[], ny, -1);
fftwplan p2 = plandfft(u[], v[], ny, 1);
real ccc = square(2.*pi);
cout << "ny = " << ny << endl;
map(wij[], ny, ccc*(x*x+y*y));
wij[][0] = 1e-5;
plot(wij, cmm="wij");

Complex

real a = 2.45, b = 5.33;
complex z1 = a + b*1i, z2 = a + sqrt(2.)*1i;

func string pc(complex z){
    string r = "(" + real(z);
    if (imag(z) >= 0) r = r + "+";
    return r + imag(z) + "i)";
}

func string toPolar(complex z){
    return "";//abs(z) + "*(cos(" + arg(z) + ")+i*sin(" + arg(z) + "))";
}

cout << "Standard output of the complex " << pc(z1) << " is the pair: " << z1 << endl;
cout << pc(z1) << " + " << pc(z2) << " = " << pc(z1+z2) << endl;
cout << pc(z1) << " - " << pc(z2) << " = " << pc(z1-z2) << endl;
cout << pc(z1) << " * " << pc(z2) << " = " << pc(z1*z2) << endl;
cout << pc(z1) << " / " << pc(z2) << " = " << pc(z1/z2) << endl;
cout << "Real part of " << pc(z1) << " = " << real(z1) << endl;
cout << "Imaginary part of " << pc(z1) << " = " << imag(z1) << endl;
cout << "abs(" << pc(z1) << ") = " << abs(z1) << endl;
cout << "Polar coordinates of " << pc(z2) << " = " << toPolar(z2) << endl;
cout << "de Moivre formula: " << pc(z2) << "^3 = " << toPolar(z2^3) << endl;
cout << " and polar(" << abs(z2) << ", " << arg(z2) << ") = " << pc(polar(abs(z2), arg(z2))) << endl;
cout << "Conjugate of " <<pc(z2) << " = " << pc(conj(z2)) <<endl;
cout << pc(z1) << " ^ " << pc(z2) << " = " << pc(z1^z2) << endl;

Output of this script is:

Standard output of the complex (2.45+5.33i) is the pair: (2.45,5.33)
(2.45+5.33i) + (2.45+1.41421i) = (4.9+6.74421i)
(2.45+5.33i) - (2.45+1.41421i) = (0+3.91579i)
(2.45+5.33i) * (2.45+1.41421i) = (-1.53526+16.5233i)
(2.45+5.33i) / (2.45+1.41421i) = (1.692+1.19883i)
Real part of (2.45+5.33i) = 2.45
Imaginary part of (2.45+5.33i) = 5.33
abs((2.45+5.33i)) = 5.86612
Polar coordinates of (2.45+1.41421i) =
de Moivre formula: (2.45+1.41421i)^3 =
 and polar(2.82887, 0.523509) = (2.45+1.41421i)
Conjugate of (2.45+1.41421i) = (2.45-1.41421i)
(2.45+5.33i) ^ (2.45+1.41421i) = (8.37072-12.7078i)

String

// Concatenation
string tt = "toto1" + 1 + " -- 77";

// Append
string t1 = "0123456789";
t1(4:3) = "abcdefghijk-";

// Sub string
string t55 = t1(4:14);

cout << "tt = " << tt << endl;

cout << "t1 = " << t1 << endl;
cout << "t1.find(abc) = " << t1.find("abc") << endl;
cout << "t1.rfind(abc) = " << t1.rfind("abc") << endl;
cout << "t1.find(abc, 10) = " << t1.find("abc",10) << endl;
cout << "t1.ffind(abc, 10) = " << t1.rfind("abc",10) << endl;
cout << "t1.length = " << t1.length << endl;

cout << "t55 = " << t55 << endl;

The output of this script is:

tt = toto11 -- 77
t1 = 0123abcdefghijk-456789
t1.find(abc) = 4
t1.rfind(abc) = 4
t1.find(abc, 10) = -1
t1.ffind(abc, 10) = 4
t1.length = 22
t55 = abcdefghijk

Elementary function

real b = 1.;
real a = b;
func real phix(real t){
    return (a+b)*cos(t) - b*cos(t*(a+b)/b);
}
func real phiy(real t){
    return (a+b)*sin(t) - b*sin(t*(a+b)/b);
}

border C(t=0, 2*pi){x=phix(t); y=phiy(t);}
mesh Th = buildmesh(C(50));
plot(Th);

Array

real[int] tab(10), tab1(10); //2 array of 10 real
//real[int] tab2; //bug: array with no size

tab = 1.03; //set all the array to 1.03
tab[1] = 2.15;

cout << "tab: " << tab << endl;
cout << "min: " << tab.min << endl;
cout << "max: " << tab.max << endl;
cout << "sum: " << tab.sum << endl;

tab.resize(12); //change the size of array tab to 12 with preserving first value
tab(10:11) = 3.14; //set values 10 & 11
cout << "resized tab: " << tab << endl;

tab.sort ; //sort the array tab
cout << "sorted tab:" << tab << endl;

real[string] tt; //array with string index
tt["+"] = 1.5;
cout << "tt[\"a\"] = " << tt["a"] << endl;
cout << "tt[\"+\"] = " << tt["+"] << endl;

real[int] a(5), b(5), c(5), d(5);
a = 1;
b = 2;
c = 3;
a[2] = 0;
d = ( a ? b : c ); //for i = 0, n-1 : d[i] = a[i] ? b[i] : c[i]
cout << " d = ( a ? b : c ) is " << d << endl;
d = ( a ? 1 : c ); //for i = 0, n-1: d[i] = a[i] ? 1 : c[i]
d = ( a ? b : 0 ); //for i = 0, n-1: d[i] = a[i] ? b[i] : 0
d = ( a ? 1 : 0 ); //for i = 0, n-1: d[i] = a[i] ? 0 : 1

int[int] ii(0:d.n-1); //set array ii to 0, 1, ..., d.n-1
d = -1:-5; //set d to -1, -2, ..., -5

sort(d, ii); //sort array d and ii in parallel
cout << "d: " << d << endl;
cout << "ii: " << ii << endl;


{
    int[int] A1(2:10); //2, 3, 4, 5, 6, 7, 8, 9, 10
    int[int] A2(2:3:10); //2, 5, 8
    cout << "A1(2:10): " << A1 << endl;
    cout << "A2(2:3:10): " << A1 << endl;
    A1 = 1:2:5;
    cout << "1:2:5 => " << A1 << endl;
}
{
    real[int] A1(2:10); //2, 3, 4, 5, 6, 7, 8, 9, 10
    real[int] A2(2:3:10); //2, 5, 8
    cout << "A1(2:10): " << A1 << endl;
    cout << "A2(2:3:10): " << A1 << endl;
    A1 = 1.:0.5:3.999;
    cout << "1.:0.5:3.999 => " << A1 << endl;
}
{
    complex[int] A1(2.+0i:10.+0i); //2, 3, 4, 5, 6, 7, 8, 9, 10
    complex[int] A2(2.:3.:10.); //2, 5, 8
    cout << " A1(2.+0i:10.+0i): " << A1 << endl;
    cout << " A2(2.:3.:10.)= " << A2 << endl;
    cout << " A1.re real part array: " << A1.re << endl ;
    // he real part array of the complex array
    cout << " A1.im imag part array: " << A1.im << endl ;
    //the imaginary part array of the complex array
}

// Integer array operators
{
    int N = 5;
    real[int] a(N), b(N), c(N);
    a = 1;
    a(0:4:2) = 2;
    a(3:4) = 4;
    cout << "a: " << a << endl;
    b = a + a;
    cout <<"b = a + a: " << b << endl;
    b += a;
    cout <<"b += a: " << b << endl;
    b += 2*a;
    cout <<"b += 2*a: " << b << endl;
    b /= 2;
    cout <<" b /= 2: " << b << endl;
    b .*= a; // same as b = b .* a
    cout << "b .*= a: " << b << endl;
    b ./= a; //same as b = b ./ a
    cout << "b ./= a: " << b << endl;
    c = a + b;
    cout << "c = a + b: " << c << endl;
    c = 2*a + 4*b;
    cout << "c = 2*a + 4b: " << c << endl;
    c = a + 4*b;
    cout << "c = a + 4b: " << c << endl;
    c = -a + 4*b;
    cout << "c = -a + 4b: " << c << endl;
    c = -a - 4*b;
    cout << "c = -a - 4b: " << c << endl;
    c = -a - b;
    cout << "c = -a -b: " << c << endl;

    c = a .* b;
    cout << "c = a .* b: " << c << endl;
    c = a ./ b;
    cout << "c = a ./ b: " << c << endl;
    c = 2 * b;
    cout << "c = 2 * b: " << c << endl;
    c = b * 2;
    cout << "c = b * 2: " << c << endl;

    //this operator do not exist
    //c = b/2;
    //cout << "c = b / 2: " << c << endl;

    //Array methods
    cout << "||a||_1 = " << a.l1 << endl;
    cout << "||a||_2 = " << a.l2 << endl;
    cout << "||a||_infty = " << a.linfty << endl;
    cout << "sum a_i = " << a.sum << endl;
    cout << "max a_i = " << a.max << " a[ " << a.imax << " ] = " << a[a.imax] << endl;
    cout << "min a_i = " << a.min << " a[ " << a.imin << " ] = " << a[a.imin] << endl;

    cout << "a' * a = " << (a'*a) << endl;
    cout << "a quantile 0.2 = " << a.quantile(0.2) << endl;

    //Array mapping
    int[int] I = [2, 3, 4, -1, 3];
    b = c = -3;
    b = a(I); //for (i = 0; i < b.n; i++) if (I[i] >= 0) b[i] = a[I[i]];
    c(I) = a; //for (i = 0; i < I.n; i++) if (I[i] >= 0) C(I[i]) = a[i];
    cout << "b = a(I) : " << b << endl;
    cout << "c(I) = a " << c << endl;
    c(I) += a; //for (i = 0; i < I.n; i++) if (I[i] >= 0) C(I[i]) += a[i];
    cout << "b = a(I) : " << b << endl;
    cout << "c(I) = a " << c << endl;

}

{
    // Array versus matrix
    int N = 3, M = 4;

    real[int, int] A(N, M);
    real[int] b(N), c(M);
    b = [1, 2, 3];
    c = [4, 5, 6, 7];

    complex[int, int] C(N, M);
    complex[int] cb = [1, 2, 3], cc = [10i, 20i, 30i, 40i];

    b = [1, 2, 3];

    int [int] I = [2, 0, 1];
    int [int] J = [2, 0, 1, 3];

    A = 1; //set all the matrix
    A(2, :) = 4; //the full line 2
    A(:, 1) = 5; //the full column 1
    A(0:N-1, 2) = 2; //set the column 2
    A(1, 0:2) = 3; //set the line 1 from 0 to 2

    cout << "A = " << A << endl;

    //outer product
    C = cb * cc';
    C += 3 * cb * cc';
    C -= 5i * cb * cc';
    cout << "C = " << C << endl;

    //this transforms an array into a sparse matrix
    matrix B;
    B = A;
    B = A(I, J); //B(i, j) = A(I(i), J(j))
    B = A(I^-1, J^-1); //B(I(i), J(j)) = A(i,j)

    //outer product
    A = 2. * b * c';
    cout << "A = " << A << endl;
    B = b*c'; //outer product B(i, j) = b(i)*c(j)
    B = b*c'; //outer product B(i, j) = b(i)*c(j)
    B = (2*b*c')(I, J); //outer product B(i, j) = b(I(i))*c(J(j))
    B = (3.*b*c')(I^-1,J^-1); //outer product B(I(i), J(j)) = b(i)*c(j)
    cout << "B = (3.*b*c')(I^-1,J^-1) = " << B << endl;

    //row and column of the maximal coefficient of A
    int i, j, ii, jj;
    ijmax(A, ii, jj);

    i = A.imax;
    j = A.jmax;

    cout << "Max " << i << " " << j << ", = " << A.max << endl;

    //row and column of the minimal coefficient of A
    ijmin(A, i, j);

    ii = A.imin;
    jj = A.jmin;

    cout << "Min " << ii << " " << jj << ", = " << A.min << endl;
}

The output os this script is:

tab: 10
    1.03    2.15    1.03    1.03    1.03
    1.03    1.03    1.03    1.03    1.03

min: 1.03
max: 2.15
sum: 11.42
resized tab: 12
    1.03    2.15    1.03    1.03    1.03
    1.03    1.03    1.03    1.03    1.03
    3.14    3.14
sorted tab:12
    1.03    1.03    1.03    1.03    1.03
    1.03    1.03    1.03    1.03    2.15
    3.14    3.14
tt["a"] = 0
tt["+"] = 1.5
 d = ( a ? b : c ) is 5
      2   2   3   2   2

d: 5
     -5  -4  -3  -2  -1

ii: 5
      4   3   2   1   0

A1(2:10): 9
      2   3   4   5   6
      7   8   9  10
A2(2:3:10): 9
      2   3   4   5   6
      7   8   9  10
1:2:5 => 3
      1   3   5
A1(2:10): 9
      2   3   4   5   6
      7   8   9  10
A2(2:3:10): 9
      2   3   4   5   6
      7   8   9  10
1.:0.5:3.999 => 6
      1 1.5   2 2.5   3
    3.5
 A1(2.+0i:10.+0i): 9
    (2,0)   (3,0)   (4,0)   (5,0)   (6,0)
    (7,0)   (8,0)   (9,0)   (10,0)
 A2(2.:3.:10.)= 3
    (2,0)   (5,0)   (8,0)
 A1.re real part array: 9
      2   3   4   5   6
      7   8   9  10
 A1.im imag part array: 9
      0   0   0   0   0
      0   0   0   0
a: 5
      2   1   2   4   4

b = a + a: 5
      4   2   4   8   8

b += a: 5
      6   3   6  12  12

b += 2*a: 5
     10   5  10  20  20

 b /= 2: 5
      5 2.5   5  10  10

b .*= a: 5
     10 2.5  10  40  40

b ./= a: 5
      5 2.5   5  10  10

c = a + b: 5
      7 3.5   7  14  14

c = 2*a + 4b: 5
     24  12  24  48  48

c = a + 4b: 5
     22  11  22  44  44

c = -a + 4b: 5
     18   9  18  36  36

c = -a - 4b: 5
    -22 -11 -22 -44 -44

c = -a -b: 5
     -7 -3.5     -7 -14 -14

c = a .* b: 5
     10 2.5  10  40  40

c = a ./ b: 5
    0.4 0.4 0.4 0.4 0.4

c = 2 * b: 5
     10   5  10  20  20

c = b * 2: 5
     10   5  10  20  20

||a||_1 = 13
||a||_2 = 6.40312
||a||_infty = 4
sum a_i = 13
max a_i = 4 a[ 3 ] = 4
min a_i = 1 a[ 1 ] = 1
a' * a = 41
a quantile 0.2 = 2
b = a(I) : 5
      2   4   4  -3   4

c(I) = a 5
     -3  -3   2   4   2

b = a(I) : 5
      2   4   4  -3   4

c(I) = a 5
     -3  -3   4   9   4

A = 3 4
       1   5   2   1
       3   3   3   1
       4   5   2   4

C = 3 4
     (-50,-40) (-100,-80) (-150,-120) (-200,-160)
     (-100,-80) (-200,-160) (-300,-240) (-400,-320)
     (-150,-120) (-300,-240) (-450,-360) (-600,-480)

A = 3 4
       8  10  12  14
      16  20  24  28
      24  30  36  42

B = (3.*b*c')(I^-1,J^-1) = # Sparse Matrix (Morse)
# first line: n m (is symmetic) nbcoef
# after for each nonzero coefficient:   i j a_ij where (i,j) \in  {1,...,n}x{1,...,m}
3 4 0  12
        1         1 10
        1         2 12
        1         3 8
        1         4 14
        2         1 15
        2         2 18
        2         3 12
        2         4 21
        3         1 5
        3         2 6
        3         3 4
        3         4 7

Block matrix

// Parameters
real f1 = 1.;
real f2 = 1.5;

// Mesh
mesh Th1 = square(10, 10);
mesh Th2 = square(10, 10, [1+x, -1+y]);
plot(Th1, Th2);

// Fespace
fespace Uh1(Th1, P1);
Uh1 u1;

fespace Uh2(Th2, P2);
Uh2 u2;

// Macro
macro grad(u) [dx(u), dy(u)] //

// Problem
varf vPoisson1 (u, v)
    = int2d(Th1)(
          grad(u)' * grad(v)
    )
    - int2d(Th1)(
          f1 * v
    )
    + on(1, 2, 3, 4, u=0)
    ;

varf vPoisson2 (u, v)
    = int2d(Th2)(
          grad(u)' * grad(v)
    )
    - int2d(Th2)(
          f1 * v
    )
    + on(1, 2, 3, 4, u=0)
    ;
matrix<real> Poisson1 = vPoisson1(Uh1, Uh1);
real[int] Poisson1b = vPoisson1(0, Uh1);

matrix<real> Poisson2 = vPoisson2(Uh2, Uh2);
real[int] Poisson2b = vPoisson2(0, Uh2);

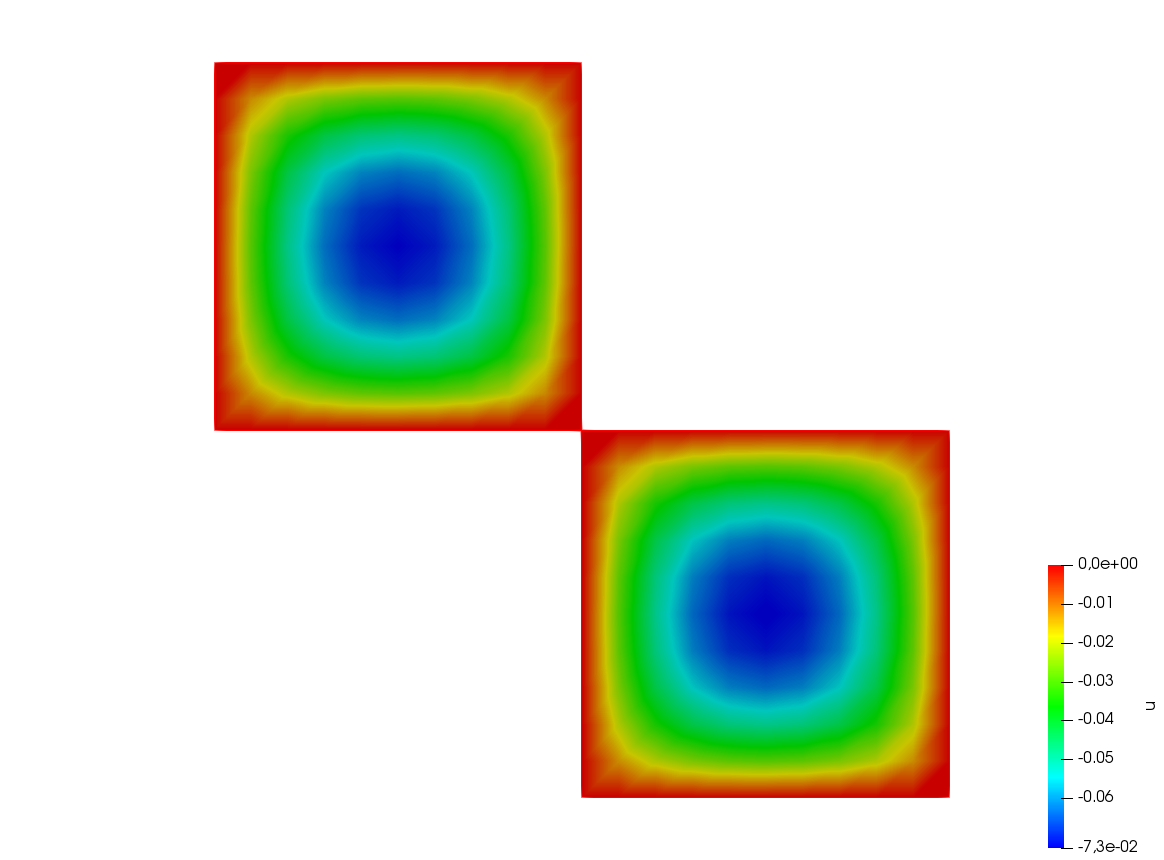
//block matrix
matrix<real> G = [[Poisson1, 0], [0, Poisson2]];
set(G, solver=sparsesolver);

//block right hand side
real[int] Gb = [Poisson1b, Poisson2b];

// Solve
real[int] sol = G^-1 * Gb;

// Dispatch
[u1[], u2[]] = sol;

// Plot
plot(u1, u2);

Matrix operations

// Mesh
mesh Th = square(2, 1);

// Fespace
fespace Vh(Th, P1);
Vh f, g;
f = x*y;
g = sin(pi*x);

Vh<complex> ff, gg; //a complex valued finite element function
ff= x*(y+1i);
gg = exp(pi*x*1i);

// Problem
varf mat (u, v)
    = int2d(Th)(
          1*dx(u)*dx(v)
        + 2*dx(u)*dy(v)
        + 3*dy(u)*dx(v)
        + 4*dy(u)*dy(v)
    )
    + on(1, 2, 3, 4, u=1)
    ;

varf mati (u, v)
    = int2d(Th)(
         1*dx(u)*dx(v)
        + 2i*dx(u)*dy(v)
        + 3*dy(u)*dx(v)
        + 4*dy(u)*dy(v)
    )
    + on(1, 2, 3, 4, u=1)
    ;

matrix A = mat(Vh, Vh);
matrix<complex> AA = mati(Vh, Vh); //a complex sparse matrix

// Operations
Vh m0; m0[] = A*f[];
Vh m01; m01[] = A'*f[];
Vh m1; m1[] = f[].*g[];
Vh m2; m2[] = f[]./g[];

// Display
cout << "f = " << f[] << endl;
cout << "g = " << g[] << endl;
cout << "A = " << A << endl;
cout << "m0 = " << m0[] << endl;
cout << "m01 = " << m01[] << endl;
cout << "m1 = "<< m1[] << endl;
cout << "m2 = "<< m2[] << endl;
cout << "dot Product = "<< f[]'*g[] << endl;
cout << "hermitien Product = "<< ff[]'*gg[] << endl;
cout << "outer Product = "<< (A=f[]*g[]') << endl;
cout << "hermitien outer Product = "<< (AA=ff[]*gg[]') << endl;

// Diagonal
real[int] diagofA(A.n);
diagofA = A.diag; //get the diagonal of the matrix
A.diag = diagofA ; //set the diagonal of the matrix

// Sparse matrix set
int[int] I(1), J(1);
real[int] C(1);

[I, J, C] = A; //get the sparse term of the matrix A (the array are resized)
cout << "I = " << I << endl;
cout << "J = " << J << endl;
cout << "C = " << C << endl;

A = [I, J, C]; //set a new matrix
matrix D = [diagofA]; //set a diagonal matrix D from the array diagofA
cout << "D = " << D << endl;

The output of this script is:

f = 6
      0   0   0   0 0.5
      1
g = 6
      0   1 1.224646799e-16   0   1
    1.224646799e-16
A = # Sparse Matrix (Morse)
# first line: n m (is symmetic) nbcoef
# after for each nonzero coefficient:   i j a_ij where (i,j) \in  {1,...,n}x{1,...,m}
6 6 0  24
        1         1 1.0000000000000000199e+30
        1         2 0.49999999999999994449
        1         4 0
        1         5 -2.5
        2         1 0
        2         2 1.0000000000000000199e+30
        2         3 0.49999999999999994449
        2         5 0.49999999999999977796
        2         6 -2.5
        3         2 0
        3         3 1.0000000000000000199e+30
        3         6 0.49999999999999977796
        4         1 0.49999999999999977796
        4         4 1.0000000000000000199e+30
        4         5 0
        5         1 -2.5
        5         2 0.49999999999999977796
        5         4 0.49999999999999994449
        5         5 1.0000000000000000199e+30
        5         6 0
        6         2 -2.5
        6         3 0
        6         5 0.49999999999999994449
        6         6 1.0000000000000000199e+30

m0 = 6
    -1.25   -2.25   0.5   0 5e+29
    1e+30
m01 = 6
    -1.25   -2.25     0 0.25    5e+29
    1e+30
m1 = 6
      0   0   0   0 0.5
    1.224646799e-16
m2 = 6
    -nan      0   0 -nan    0.5
    8.165619677e+15
dot Product = 0.5
hermitien Product = (1.11022e-16,2.5)
outer Product = # Sparse Matrix (Morse)
# first line: n m (is symmetic) nbcoef
# after for each nonzero coefficient:   i j a_ij where (i,j) \in  {1,...,n}x{1,...,m}
6 6 0  8
        5         2 0.5
        5         3 6.1232339957367660359e-17
        5         5 0.5
        5         6 6.1232339957367660359e-17
        6         2 1
        6         3 1.2246467991473532072e-16
        6         5 1
        6         6 1.2246467991473532072e-16

hermitien outer Product = # Sparse Matrix (Morse)
# first line: n m (is symmetic) nbcoef
# after for each nonzero coefficient:   i j a_ij where (i,j) \in  {1,...,n}x{1,...,m}
6 6 0  24
        2         1 (0,0.5)
        2         2 (0.5,3.0616169978683830179e-17)
        2         3 (6.1232339957367660359e-17,-0.5)
        2         4 (0,0.5)
        2         5 (0.5,3.0616169978683830179e-17)
        2         6 (6.1232339957367660359e-17,-0.5)
        3         1 (0,1)
        3         2 (1,6.1232339957367660359e-17)
        3         3 (1.2246467991473532072e-16,-1)
        3         4 (0,1)
        3         5 (1,6.1232339957367660359e-17)
        3         6 (1.2246467991473532072e-16,-1)
        5         1 (0.5,0.5)
        5         2 (0.5,-0.49999999999999994449)
        5         3 (-0.49999999999999994449,-0.50000000000000011102)
        5         4 (0.5,0.5)
        5         5 (0.5,-0.49999999999999994449)
        5         6 (-0.49999999999999994449,-0.50000000000000011102)
        6         1 (1,1)
        6         2 (1,-0.99999999999999988898)
        6         3 (-0.99999999999999988898,-1.000000000000000222)
        6         4 (1,1)
        6         5 (1,-0.99999999999999988898)
        6         6 (-0.99999999999999988898,-1.000000000000000222)

I = 8
      4   4   4   4   5
      5   5   5
J = 8
      1   2   4   5   1
      2   4   5
C = 8
    0.5 6.123233996e-17 0.5 6.123233996e-17   1
    1.224646799e-16   1 1.224646799e-16
  -- Raw Matrix    nxm  =6x6 nb  none zero coef. 8
  -- Raw Matrix    nxm  =6x6 nb  none zero coef. 6
D = # Sparse Matrix (Morse)
# first line: n m (is symmetic) nbcoef
# after for each nonzero coefficient:   i j a_ij where (i,j) \in  {1,...,n}x{1,...,m}
6 6 1  6
        1         1 0
        2         2 0
        3         3 0
        4         4 0
        5         5 0.5
        6         6 1.2246467991473532072e-16

Warning

Due to Fortran indices starting at one, the output of a diagonal matrix D is indexed from 1. but in FreeFEM, the indices start from 0.

Matrix inversion

load "lapack"
load "fflapack"

// Matrix
int n = 5;
real[int, int] A(n, n), A1(n, n), B(n,n);
for (int i = 0; i < n; ++i)
    for (int j = 0; j < n; ++j)
        A(i, j) = (i == j) ? n+1 : 1;
cout << A << endl;

// Inversion (lapack)
A1 = A^-1; //def in "lapack"
cout << A1 << endl;

B = 0;
for (int i = 0; i < n; ++i)
    for (int j = 0; j < n; ++j)
        for (int k = 0; k < n; ++k)
            B(i, j) += A(i,k)*A1(k,j);
cout << B << endl;

// Inversion (fflapack)
inv(A1); //def in "fflapack"
cout << A1 << endl;

The output of this script is:

5 5
       6   1   1   1   1
       1   6   1   1   1
       1   1   6   1   1
       1   1   1   6   1
       1   1   1   1   6

5 5
     0.18 -0.02 -0.02 -0.02 -0.02
     -0.02 0.18 -0.02 -0.02 -0.02
     -0.02 -0.02 0.18 -0.02 -0.02
     -0.02 -0.02 -0.02 0.18 -0.02
     -0.02 -0.02 -0.02 -0.02 0.18

5 5
       1 1.040834086e-17 1.040834086e-17 1.734723476e-17 2.775557562e-17
     3.469446952e-18   1 -1.734723476e-17 1.734723476e-17 2.775557562e-17
     2.428612866e-17 -3.122502257e-17   1 1.734723476e-17 2.775557562e-17
     2.081668171e-17 -6.938893904e-17 -3.469446952e-17   1   0
     2.775557562e-17 -4.163336342e-17 -2.775557562e-17   0   1

5 5
       6   1   1   1   1
       1   6   1   1   1
       1   1   6   1   1
       1   1   1   6   1
       1   1   1   1   6

Tip

To compile lapack.cpp and fflapack.cpp, you must have the lapack library on your system and compile the plugin with the command:

ff-c++ lapack.cpp -llapack     ff-c++ fflapack.cpp -llapack

FE array

// Mesh
mesh Th = square(20, 20, [2*x, 2*y]);

// Fespace
fespace Vh(Th, P1);
Vh u, v, f;

// Problem
problem Poisson (u, v)
    = int2d(Th)(
          dx(u)*dx(v)
        + dy(u)*dy(v)
    )
    + int2d(Th)(
        - f*v
    )
    + on(1, 2, 3, 4, u=0)
    ;

Vh[int] uu(3); //an array of FE function
// Solve problem 1
f = 1;
Poisson;
uu[0] = u;
// Solve problem 2
f = sin(pi*x)*cos(pi*y);
Poisson;
uu[1] = u;
// Solve problem 3
f = abs(x-1)*abs(y-1);
Poisson;
uu[2] = u;

// Plot
for (int i = 0; i < 3; i++)
    plot(uu[i], wait=true);

Finite element array

Loop

for (int i = 0; i < 10; i=i+1)
    cout << i << endl;

real eps = 1.;
while (eps > 1e-5){
    eps = eps/2;
    if (i++ < 100)
        break;
    cout << eps << endl;
}

for (int j = 0; j < 20; j++){
    if (j < 10) continue;
    cout << "j = " << j << endl;
}

Implicit loop

real [int, int] a(10, 10);
real [int] b(10);

for [i, bi : b]{
    bi = i+1;
    cout << i << " " << bi << endl;
}
cout << "b = " << b << endl;

for [i, j, aij : a]{
    aij = 1./(2+i+j);
    if (abs(aij) < 0.2) aij = 0;
}
cout << "a = " << a << endl;

matrix A = a;
string[string] ss; //a map
ss["1"] = 1;
ss["2"] = 2;
ss["3"] = 5;
for [i, bi : ss]
    bi = i + 6 + "-dddd";
cout << "ss = " << ss << endl;

int[string] si;
si[1] = 2;
si[50] = 1;
for [i, vi : si]{
    cout << " i " << setw(3) << i << " " << setw(10) << vi << endl;
    vi = atoi(i)*2;
}
cout << "si = " << si << endl;

for [i, j, aij : A]{
    cout << i << " " << j << " " << aij << endl;
    aij = -aij;
}
cout << A << endl;

The output of this script is:

0 1
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
b = 10
      1   2   3   4   5
      6   7   8   9  10

a = 10 10
     0.5 0.3333333333 0.25 0.2   0   0   0   0   0   0
     0.3333333333 0.25 0.2   0   0   0   0   0   0   0
     0.25 0.2   0   0   0   0   0   0   0   0
     0.2   0   0   0   0   0   0   0   0   0
       0   0   0   0   0   0   0   0   0   0
       0   0   0   0   0   0   0   0   0   0
       0   0   0   0   0   0   0   0   0   0
       0   0   0   0   0   0   0   0   0   0
       0   0   0   0   0   0   0   0   0   0
       0   0   0   0   0   0   0   0   0   0

ss = 1 1
2 2
3 5

 i   1          2
 i  50          1
si = 1 2
50 100

0 0 0.5
0 1 0.333333
0 2 0.25
0 3 0.2
1 0 0.333333
1 1 0.25
1 2 0.2
2 0 0.25
2 1 0.2
3 0 0.2
# Sparse Matrix (Morse)
# first line: n m (is symmetic) nbcoef
# after for each nonzero coefficient:   i j a_ij where (i,j) \in  {1,...,n}x{1,...,m}
10 10 0  10
        1         1 -0.5
        1         2 -0.33333333333333331483
        1         3 -0.25
        1         4 -0.2000000000000000111
        2         1 -0.33333333333333331483
        2         2 -0.25
        2         3 -0.2000000000000000111
        3         1 -0.25
        3         2 -0.2000000000000000111
        4         1 -0.2000000000000000111

I/O

int i;
cout << "std-out" << endl;
cout << " enter i = ?";
cin >> i;

{
    ofstream f("toto.txt");
    f << i << "hello world'\n";
} //close the file f because the variable f is delete

{
    ifstream f("toto.txt");
    f >> i;
}

{
    ofstream f("toto.txt", append);
    //to append to the existing file "toto.txt"
    f << i << "hello world'\n";
} //close the file f because the variable f is delete

cout << i << endl;

File stream

int where;
real[int] f = [0, 1, 2, 3, 4, 5];
real[int] g(6);

{
    ofstream file("f.txt", binary);
    file.precision(16);
    file << f << endl;
    where = file.tellp();
    file << 0.1 ;

    cout << "Where in file " << where << endl;
    file << " # comment bla bla ... 0.3 \n";
    file << 0.2 << endl;
    file.flush; //to flush the buffer of file
}

//Function to skip comment starting with # in a file
func ifstream skipcomment(ifstream &ff){
    while(1){
        int where = ff.tellg(); //store file position
        string comment;
        ff >> comment;
        if (!ff.good()) break;
        if (comment(0:0)=="#"){
            getline(ff, comment);
            cout << " -- #" << comment << endl;
        }
        else{
            ff.seekg(where); //restore file position
            break;
        }
    }
    return ff;
}

{
    real xx;
    ifstream file("f.txt", binary);
    cout << "Where " << file.seekg << endl;
    file.seekg(where);
    file >> xx;
    cout << " xx = " << xx << " good ? " << file.good() << endl;
    assert(xx == 0.1);
    skipcomment(file) >> xx;
    assert(xx == 0.2);
    file.seekg(0); //rewind
    cout << "Where " << file.tellg() << " " << file.good() << endl;
    file >> g;
}

Command line arguments

When using the command:

FreeFem++ script.edp arg1 arg2

The arguments can be used in the script with:

for (int i = 0; i < ARGV.n; i++)
    cout << ARGV[i] << endl;

When using the command:

FreeFem++ script.edp -n 10 -a 1. -d 42.

The arguments can be used in the script with:

include "getARGV.idp"

int n = getARGV("-n", 1);
real a = getARGV("-a", 1.);
real d = getARGV("-d", 1.);

Macro

// Macro without parameters
macro xxx() {
    real i = 0;
    int j = 0;
    cout << i << " " << j << endl;
}//

xxx

// Macro with parameters
macro toto(i) i //

toto({real i = 0; int j = 0; cout << i << " " << j << endl;})

// Macro as parameter of a macro
real[int,int] CC(7, 7), EE(6, 3), EEps(4, 4);

macro VIL6(v, i) [v(1,i), v(2,i), v(4,i), v(5,i), v(6,i)] //
macro VIL3(v, i) [v(1,i), v(2,i)] //
macro VV6(v, vv) [
    v(vv,1), v(vv,2),
    v(vv,4), v(vv,5),
    v(vv,6)] //
macro VV3(v, vv) [v(vv,1), v(vv,2)] //

func C5x5 = VV6(VIL6, CC);
func E5x2 = VV6(VIL3, EE);
func Eps = VV3(VIL3, EEps);

// Macro concatenation
mesh Th = square(2, 2);
fespace Vh(Th, P1);
Vh Ux=x, Uy=y;

macro div(V) (dx(V#x) + dy(V#y)) //

cout << int2d(Th)(div(U)) << endl;

// Verify the quoting
macro foo(i, j, k) i j k //
foo(, , )
foo({int[}, {int] a(10}, {);})

//NewMacro - EndMacro
NewMacro grad(u) [dx(u), dy(u)] EndMacro
cout << int2d(Th)(grad(Ux)' * grad(Uy)) << endl;

// IFMACRO - ENDIFMACRO
macro AA CAS1 //

IFMACRO(AA,CAS1 )
cout << "AA = " << Stringification(AA) << endl;
macro CASE file1.edp//
ENDIFMACRO
IFMACRO(AA, CAS2)
macro CASE file2.edp//
ENDIFMACRO

cout << "CASE = " << Stringification(CASE) << endl;

IFMACRO(CASE)
include Stringification(CASE)
ENDIFMACRO

// FILE - LINE
cout << "In " << FILE << ", line " << LINE << endl;

The output script generated with macros is:

: // Macro without parameters
:  macro xxx {
:     real i = 0;
:     int j = 0;
:     cout << i << " " << j << endl;
: }//
:
:
:
:
:
:  {
:     real i = 0;
:     int j = 0;
:     cout << i << " " << j << endl;
: }
:
: // Macro with parameters
:  macro toto(i )   i //
:
:                    real i = 0; int j = 0; cout << i << " " << j << endl;
:
: // Macro as parameter of a macro
: real[int,int] CC(7, 7), EE(6, 3), EEps(4, 4);
:
:   macro VIL6(v,i )   [v(1,i), v(2,i), v(4,i), v(5,i), v(6,i)] //
:   macro VIL3(v,i )   [v(1,i), v(2,i)] //
:   macro VV6(v,vv )   [
:    v(vv,1), v(vv,2),
:    v(vv,4), v(vv,5),
:    v(vv,6)] //
:   macro VV3(v,vv )   [v(vv,1), v(vv,2)] //
:
: func C5x5 =
:
:
:       [
:             [ CC(1,1),  CC(2,1),  CC(4,1),  CC(5,1),  CC(6,1)] ,         [ CC(1,2),  CC(2,2),  CC(4,2),  CC(5,2),  CC(6,2)] ,
:             [ CC(1,4),  CC(2,4),  CC(4,4),  CC(5,4),  CC(6,4)] ,         [ CC(1,5),  CC(2,5),  CC(4,5),  CC(5,5),  CC(6,5)] ,
:             [ CC(1,6),  CC(2,6),  CC(4,6),  CC(5,6),  CC(6,6)] ] ;
: func E5x2 =
:
:
:       [
:          [ EE(1,1),  EE(2,1)] ,      [ EE(1,2),  EE(2,2)] ,
:          [ EE(1,4),  EE(2,4)] ,      [ EE(1,5),  EE(2,5)] ,
:          [ EE(1,6),  EE(2,6)] ] ;
: func Eps =      [     [ EEps(1,1),  EEps(2,1)] ,      [ EEps(1,2),  EEps(2,2)] ] ;
:
: // Macro concatenation
: mesh Th = square(2, 2);
: fespace Vh(Th, P1);
: Vh Ux=x, Uy=y;
:
:  macro div(V )   (dx(V#x) + dy(V#y)) //
:
: cout << int2d(Th)(     (dx(Ux) + dy(Uy)) ) << endl;
:
: // Verify the quoting
:    macro foo(i,j,k )   i j k //
:
:         int[ int] a(10 );
:
: //NewMacro - EndMacro
:  macro grad(u )   [dx(u), dy(u)]
: cout << int2d(Th)(    [dx(Ux), dy(Ux)] ' *     [dx(Uy), dy(Uy)] ) << endl;
:
: // IFMACRO - ENDIFMACRO
:   macro AACAS1 //
:
:
: cout << "AA = " << Stringification( CAS1 ) << endl;
:   macro CASEfile1.edp//
:
:
:
: cout << "CASE = " << Stringification(file1.edp) << endl;
:
:
: include Stringification(file1.edp)cout << "This is the file 1" << endl;
:
:
:
: // FILE - LINE
: cout << "In " << FILE << ", line " << LINE << endl;

The output os this script is:

AA = CAS1
CASE = file1.edp
This is the file 1
In Macro.edp, line 59

Basic error handling

real a;
try{
    a = 1./0.;
}
catch (...) //all exceptions can be caught
{
    cout << "Catch an ExecError" << endl;
    a = 0.;
}

The output of this script is:

1/0 : d d d
  current line = 3
Exec error :  Div by 0
   -- number :1
Catch an ExecError

Error handling

// Parameters
int nn = 5;
func f = 1; //right hand side function
func g = 0; //boundary condition function

// Mesh
mesh Th = square(nn, nn);

// Fespace
fespace Vh(Th, P1);
Vh uh, vh;

// Problem
real cpu = clock();
problem laplace (uh, vh, solver=Cholesky, tolpivot=1e-6)
    = int2d(Th)(
          dx(uh)*dx(vh)
        + dy(uh)*dy(vh)
    )
    + int2d(Th)(
        - f*vh
    )
    ;

try{
    cout << "Try Cholesky" << endl;

    // Solve
    laplace;

    // Plot
    plot(uh);

    // Display
    cout << "laplacian Cholesky " << nn << ", x_" << nn << " : " << -cpu+clock() << " s, max = " << uh[].max << endl;
}
catch(...) { //catch all error
    cout << " Catch cholesky PB " << endl;
}

The output of this script is:

Try Cholesky
ERREUR choleskypivot (35)= -6.43929e-15 < 1e-06
  current line = 29
Exec error : FATAL ERREUR dans ./../femlib/MatriceCreuse_tpl.hpp
cholesky line:
   -- number :688
 catch an erreur in  solve  =>  set  sol = 0 !!!!!!!
 Catch cholesky PB

Here you can use the search bar to search in all FreeFEM examples instead

The list of all matching examples on the right is updated for each new query

Clicking on a search hit or on an example on the right brings up the corresponding script from GitHub

You can also filter the list on the right by selecting one or more intersecting categories on the left tree

Developers

FFT

Complex

String

Elementary function

Array

Block matrix

Matrix operations

Matrix inversion

FE array

Loop

Implicit loop

I/O

File stream

Command line arguments

Macro

Basic error handling

Error handling