A Flow with Shocks
Compressible Euler equations should be discretized with Finite Volumes or FEM with flux up-winding scheme but these are not implemented in FreeFEM. Nevertheless acceptable results can be obtained with the method of characteristics provided that the mean values \(\displaystyle \bar f=\frac12\left(f^++f^-\right)\) are used at shocks in the scheme, and finally mesh adaptation. As an example, consider the simplified system:
(6)\[\begin{split}\begin{array}{rcl}
\partial_t\rho+\bar u\nabla\rho + \nabla\cdot u &=& 0\nonumber\\
\partial_t u+ \bar u\nabla u +\nabla \rho &=& 0\nonumber\\
\end{array}\end{split}\]
One possibility is to couple \(u,p\) and then update \(\rho\), i.e.:
(7)\[\begin{split}\begin{array}{rcl}
\frac{1}{\delta t} (\rho^{m+1}-\rho^m \circ X^m) + \nabla\cdot u^{m+1} &=& 0\nonumber\\
\frac{1}{\delta t}(u^{m+1}-u^m \circ {\tilde X}^m ) +\nabla \rho^{m+1} &=& 0\nonumber\\
\end{array}\end{split}\]
A numerical result is given on Fig. 42 and the FreeFEM script is
1// Parameters
2verbosity = 1;
3int anew = 1;
4int m = 5;
5real x0 = 0.5;
6real y0 = 0.;
7real rr = 0.2;
8real dt = 0.01;
9real u0 = 2.;
10real err0 = 0.00625;
11real pena = 2.;
12
13// Mesh
14border ccc(t=0, 2){x=2-t; y=1;};
15border ddd(t=0, 1){x=0; y=1-t;};
16border aaa1(t=0, x0-rr){x=t; y=0;};
17border cercle(t=pi, 0){x=x0+rr*cos(t); y=y0+rr*sin(t);}
18border aaa2(t=x0+rr, 2){x=t; y=0;};
19border bbb(t=0, 1){x=2; y=t;};
20
21 mesh Th;
22if(anew)
23 Th = buildmesh (ccc(5*m) + ddd(3*m) + aaa1(2*m) + cercle(5*m) + aaa2(5*m) + bbb(2*m));
24else
25 Th = readmesh("Th_circle.mesh"); plot(Th);
26
27// fespace
28fespace Wh(Th, P1);
29Wh u, v;
30Wh u1, v1;
31Wh uh, vh;
32
33fespace Vh(Th, P1);
34Vh r, rh, r1;
35
36// Macro
37macro dn(u) (N.x*dx(u)+N.y*dy(u)) //
38
39// Initialization
40if(anew){
41 u1 = u0;
42 v1 = 0;
43 r1 = 1;
44}
45else{
46 ifstream g("u.txt"); g >> u1[];
47 ifstream gg("v.txt"); gg >> v1[];
48 ifstream ggg("r.txt"); ggg >> r1[];
49 plot(u1, ps="eta.eps", value=1, wait=1);
50 err0 = err0/10;
51 dt = dt/10;
52}
53
54// Problem
55problem euler(u, v, r, uh, vh, rh)
56 = int2d(Th)(
57 (u*uh + v*vh + r*rh)/dt
58 + ((dx(r)*uh + dy(r)*vh) - (dx(rh)*u + dy(rh)*v))
59 )
60 + int2d(Th)(
61 - (
62 rh*convect([u1,v1],-dt,r1)
63 + uh*convect([u1,v1],-dt,u1)
64 + vh*convect([u1,v1],-dt,v1)
65 )/dt
66 )
67 +int1d(Th, 6)(
68 rh*u
69 )
70 + on(2, r=0)
71 + on(2, u=u0)
72 + on(2, v=0)
73 ;
74
75// Iterations
76int j = 80;
77for(int k = 0; k < 3; k++){
78 if(k==20){
79 err0 = err0/10;
80 dt = dt/10;
81 j = 5;
82 }
83
84 // Solve
85 for(int i = 0; i < j; i++){
86 euler;
87 u1=u;
88 v1=v;
89 r1=abs(r);
90 cout << "k = " << k << " E = " << int2d(Th)(u^2+v^2+r) << endl;
91 plot(r, value=1);
92 }
93
94 // Mesh adaptation
95 Th = adaptmesh (Th, r, nbvx=40000, err=err0, abserror=1, nbjacoby=2, omega=1.8, ratio=1.8, nbsmooth=3, splitpbedge=1, maxsubdiv=5, rescaling=1);
96 plot(Th);
97 u = u;
98 v = v;
99 r = r;
100
101 // Save
102 savemesh(Th, "Th_circle.mesh");
103 ofstream f("u.txt"); f << u[];
104 ofstream ff("v.txt"); ff << v[];
105 ofstream fff("r.txt"); fff << r[];
106 r1 = sqrt(u*u+v*v);
107 plot(r1, ps="mach.eps", value=1);
108 r1 = r;
109}
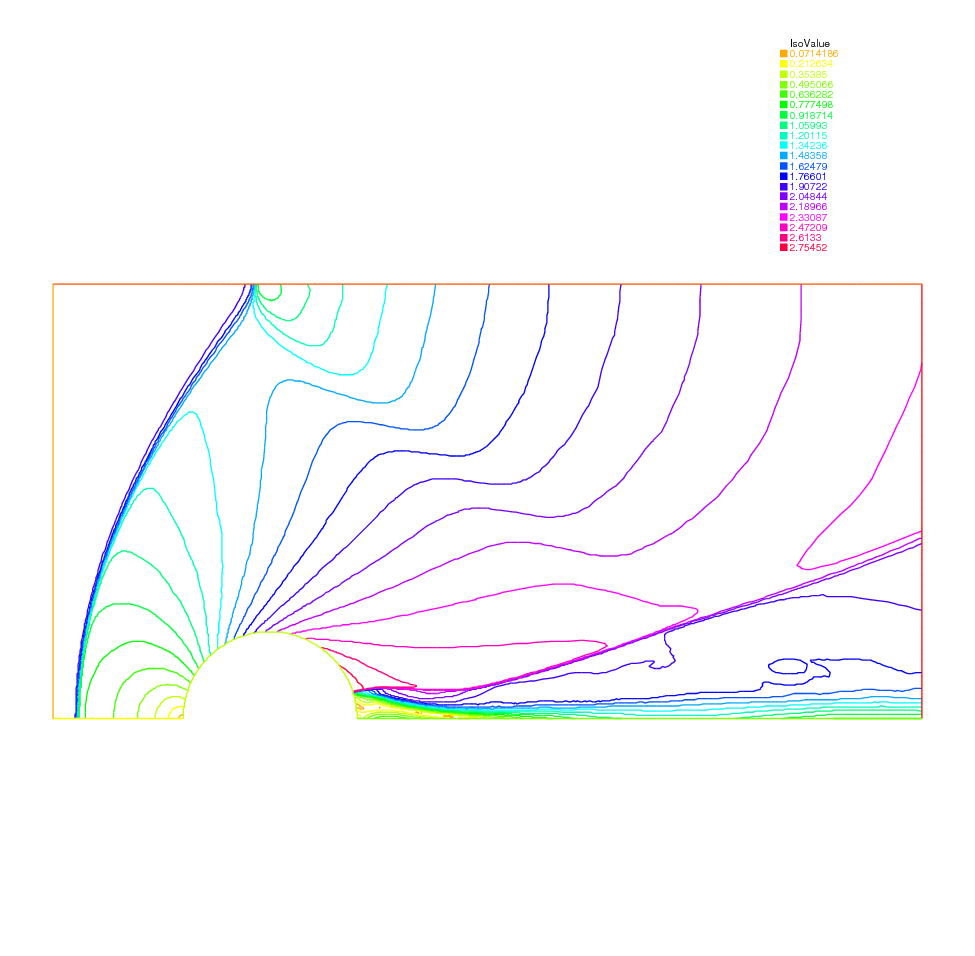
Fig. 42 Pressure for a Euler flow around a disk at Mach 2 computed by (7)
