Free boundary problems
The domain \(\Omega\) is defined with:
1// Parameters
2real L = 10; //length
3real hl = 2.1; //left height
4real hr = 0.35; //right height
5int n = 4;
6
7// Mesh
8border a(t=0, L){x=t; y=0;}; //bottom: Gamma_a
9border b(t=0, hr){x=L; y=t;}; //right: Gamma_b
10border f(t=L, 0){x=t; y=t*(hr-hl)/L+hl;}; //free surface: Gamma_f
11border d(t=hl, 0){x=0; y=t;}; // left: Gamma_d
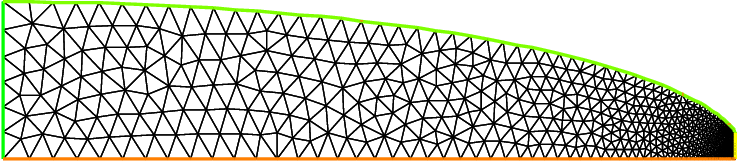
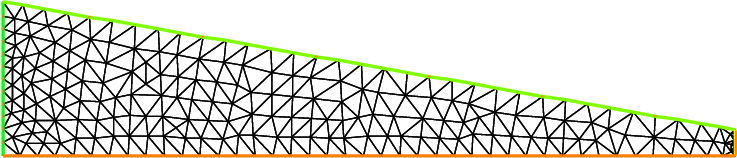
12mesh Th = buildmesh(a(10*n) + b(6*n) + f(8*n) + d(3*n));
13plot(Th);
The free boundary problem is:
Find \(u\) and \(\Omega\) such that:
\[\begin{split}\left\{
\begin{array}{rcll}
-\Delta u &=& 0 & \mbox{ in }\Omega\\
u &=& y & \mbox{ on }\Gamma_b\\
\partial u \over \partial n &=& 0 & \mbox{ on }\Gamma_d\cup\Gamma_a\\
\partial u \over \partial n &=& {q \over K} n_x & \mbox{ on }\Gamma_f\\
u &=& y & \mbox{ on }\Gamma_f
\end{array}
\right.\end{split}\]
We use a fixed point method;
\(\Omega^0 = \Omega\)
In two step, fist we solve the classical following problem:
\[\begin{split}\left\{
\begin{array}{rcll}
-\Delta u &=& 0 & \mbox{ in }\Omega^n\\
u &=& y & \mbox{ on }\Gamma^n_b\\
\partial u \over \partial n &=& 0 & \mbox{ on }\Gamma^n_d\cup\Gamma^n_a\\
u &=& y & \mbox{ on }\Gamma^n_f
\end{array}
\right.\end{split}\]
The variational formulation is:
Find \(u\) on \(V=H^1(\Omega^n)\), such than \(u=y\) on \(\Gamma^n_b\) and \(\Gamma^n_f\)
\[\int_{\Omega^n}\nabla u \nabla u' = 0,\ \forall u' \in V \mbox{ with } u' =0 \mbox{ on }\Gamma^n_b \cup \Gamma^n_f\]
And secondly to construct a domain deformation \(\mathcal{F}(x,y)=[x,y-v(x,y)]\) where \(v\) is solution of the following problem:
\[\begin{split}\left\{
\begin{array}{rcll}
-\Delta v &=& 0 & \mbox{ in }\Omega^n\\
v &=& 0 & \mbox{ on }\Gamma^n_a\\
\partial v \over \partial n &=& 0 & \mbox{ on }\Gamma^n_b\cup\Gamma^n_d\\
\partial v \over \partial n &=& {\partial u \over \partial n} - {q\over K} n_x & \mbox{ on }\Gamma^n_f
\end{array}
\right.\end{split}\]
The variational formulation is:
Find \(v\) on \(V\), such than \(v=0\) on \(\Gamma^n_a\):
\[\int_{\Omega^n} \nabla v \nabla v' = \int_{\Gamma_f^n}({\partial u \over \partial n} - { q\over K} n_x )v',\ \quad \forall v' \in V \mbox{ with } v' =0 \mbox{ on }\Gamma^n_a\]
Finally the new domain \(\Omega^{n+1} = \mathcal{F}(\Omega^n)\)
Tip
Free boundary
The FreeFEM implementation is:
1// Parameters
2real L = 10; //length
3real hr = 2.1; //left height
4real hl = 0.35; //right height
5int n = 4;
6
7real q = 0.02; //incoming flow
8real K = 0.5; //permeability
9
10// Mesh
11border a(t=0, L){x=t; y=0;}; //bottom: Gamma_a
12border b(t=0, hr){x=L; y=t;}; //right: Gamma_b
13border f(t=L, 0){x=t; y=t*(hr-hl)/L+hl;}; //free surface: Gamma_f
14border d(t=hl, 0){x=0; y=t;}; // left: Gamma_d
15mesh Th = buildmesh(a(10*n) + b(6*n) + f(8*n) + d(3*n));
16plot(Th);
17
18// Fespace
19fespace Vh(Th, P1);
20Vh u, v;
21Vh uu, vv;
22
23// Problem
24problem Pu (u, uu, solver=CG)
25 = int2d(Th)(
26 dx(u)*dx(uu)
27 + dy(u)*dy(uu)
28 )
29 + on(b, f, u=y)
30 ;
31
32problem Pv (v, vv, solver=CG)
33 = int2d(Th)(
34 dx(v)*dx(vv)
35 + dy(v)*dy(vv)
36 )
37 + on(a, v=0)
38 + int1d(Th, f)(
39 vv*((q/K)*N.y - (dx(u)*N.x + dy(u)*N.y))
40 )
41 ;
42
43// Loop
44int j = 0;
45real errv = 1.;
46real erradap = 0.001;
47while (errv > 1e-6){
48 // Update
49 j++;
50
51 // Solve
52 Pu;
53 Pv;
54
55 // Plot
56 plot(Th, u, v);
57
58 // Error
59 errv = int1d(Th, f)(v*v);
60
61 // Movemesh
62 real coef = 1.;
63 real mintcc = checkmovemesh(Th, [x, y])/5.;
64 real mint = checkmovemesh(Th, [x, y-v*coef]);
65
66 if (mint < mintcc || j%10==0){ //mesh too bad => remeshing
67 Th = adaptmesh(Th, u, err=erradap);
68 mintcc = checkmovemesh(Th, [x, y])/5.;
69 }
70
71 while (1){
72 real mint = checkmovemesh(Th, [x, y-v*coef]);
73
74 if (mint > mintcc) break;
75
76 cout << "min |T| = " << mint << endl;
77 coef /= 1.5;
78 }
79
80 Th=movemesh(Th, [x, y-coef*v]);
81
82 // Display
83 cout << endl << j << " - errv = " << errv << endl;
84}
85
86// Plot
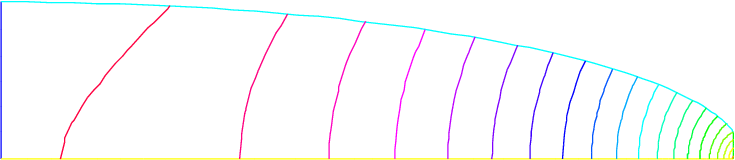
87plot(Th);
88plot(u, wait=true);