Functions

abs

Return the absolute value.

real a = abs(b);

Parameters:

b (int, real, complex, fespace function, real[int] or real[int, int])

Output:

a (int, real, real[int] or real[int, int])

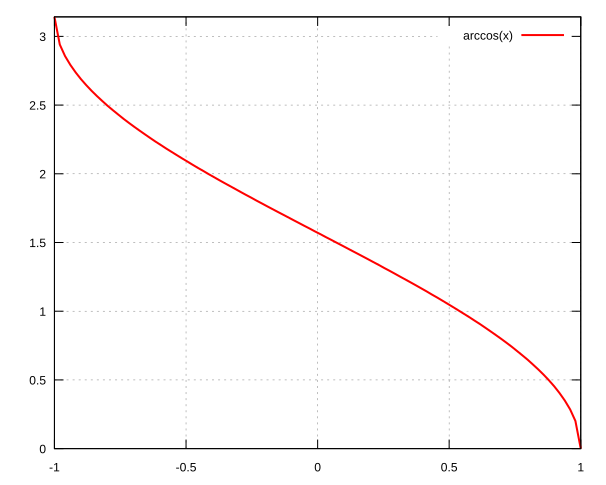
acos

\(\arccos\) function.

real theta = acos(x);

Parameter:

x (real, real[int] or real[int, int])

Output:

theta (real, real[int] or real[int, int])

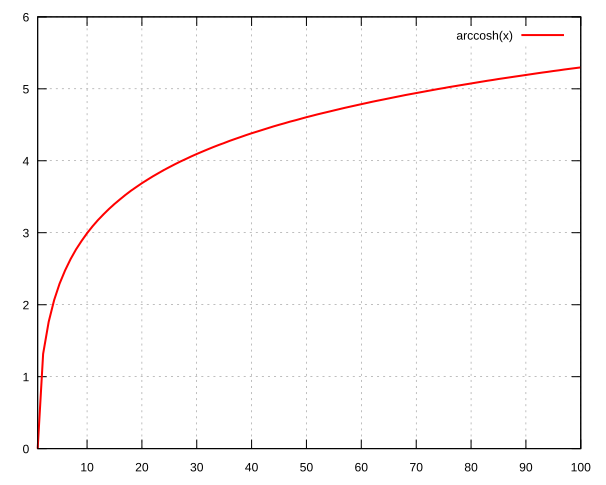
acosh

real theta = acosh(x);

\[\arccosh(x) = \ln\left(x + \sqrt{x^2-1}\right)\]

Parameter:

x (real)

Output:

theta (real)

adaptmesh

Mesh adaptation function.

mesh Thnew = adaptmesh(Th, [fx, fy], hmin=HMin, hmax=HMax, err=Err, errg=ErrG, nbvx=NbVx, nbsmooth=NbSmooth, nbjacoby=NbJacoby, ratio=Ratio, omega=Omega, iso=Iso, abserror=AbsError, cutoff=CutOff, verbosity=Verbosity, inquire=Inquire, splitpbedge=SplitPbEdge, maxsubdiv=MaxSubdiv, rescaling=Rescaling, keepbackvertices=KeepBackVertices, IsMetric=isMetric, power=Power, thetamax=ThetaMax, splitin2=SplitIn2, metric=Metric, nomeshgeneration=NoMeshGeneration, periodic=Periodic);

Parameters:

Th (mesh) Mesh to refine
[fx, fy] (func or fespace function), scalar or vectorial Function to follow for the mesh adaptation
hmin= (real) Minimum edge size
hmax= (real) Maximum edge size
err= (real) Error level (P1 interpolation)
errg= (real) Relative geometrical error
nbvx= (int) Maximum number of vertices
nbsmooth= (int) Number of smoothing iterations
nbjacoby= (int) Number of iterations for the smoothing procedure
ratio= (real) Ratio of the triangles
omega= (real) Relaxation parameter for the smoothing procedure
iso= (bool) Isotropic adaptation (if true)
abserror= (bool) Error (if true) - Relative error (if false)
cutoff= (real) Lower limit of the relative error evaluation
verbosity= (real) Verbosity level
inquire= (bool) If true, inquire graphically
splitpbedge= (bool) If true, split all internal edges in half
maxsubdiv= (int) Bound the maximum subdivisions
rescaling= (bool) Rescale the function in [0, 1]
keepbackvertices= (bool) If true, try to keep vertices of the original mesh
IsMetric= (bool) If true, the metric is defined explicitly
power= (int) Exponent of the Hessian
thetamax= (int) Minimum corner angle (in degree)
splitin2= (bool) Split all triangles into 4 sub-triangles if true
metric= ([real[int], real[int], real[int]]) Array of 3 real arrays defining the metric
nomeshgeneration= (bool) If true, the mesh is not generated
periodic= (real[int, int]) Build an adapted periodic mesh

Output:

Thnew (mesh or mesh3)

adj

Adjacent triangle of the triangle \(k\) by the edge \(e\)

int T = Th[k].adj(e);

Parameter:

e (int) Edge number

Output:

T (int) Triangle number

AffineCG

Affine conjugate gradient solver

Used to solve a problem like \(Ax=b\)

int Conv = AffineCG(A, x, precon=Precon, nbiter=NbIter, eps=Eps, veps=VEps, stop=Stop);

Parameters:

A (matrix) Matrix of the problem \(Ax=b\)
x (real[int]) Solution vector
precon= (real[int]) Preconditionning function
nbiter= (int) Maximum number of iterations
eps= (real)

Convergence criterion

If \(\varepsilon>0\): test \(||A(x)||_p \leq \epsilon||A(x_0)||_p\)

If \(\varepsilon<0\): test \(||A(x)||_p^2 \leq |\epsilon|\)
veps= (real) Same as eps, but return -eps
stop= (func) Convergence criterion as a function

Prototype is func bool StopFunc (int Iter, real[int] U, real[int] g)

u: current solution, g: current gradient (not preconditionned)

Output:

Conv (int) 0: converged - !0: not converged

AffineGMRES

Affine GMRES solver

Parameters and output are the same as AffineCG

arg

Return the argument of a complex number.

real a = arg(c);

Parameters:

c (complex)

Output:

r (real)

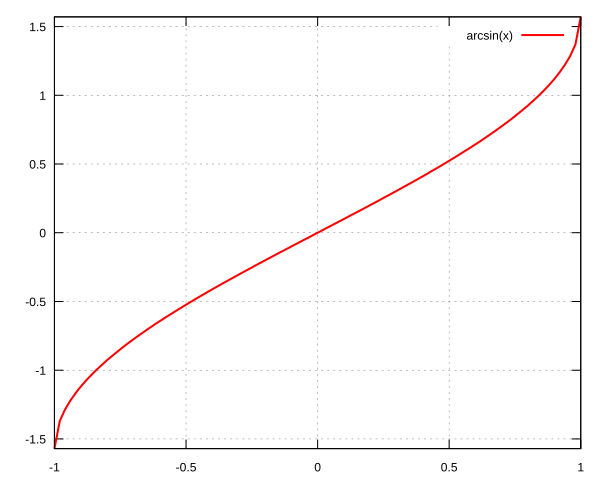
asin

\(\arcsin\) function.

real theta = asin(x);

Parameter:

x (real, real[int] or real[int, int])

Output:

theta (real, real[int] or real[int, int])

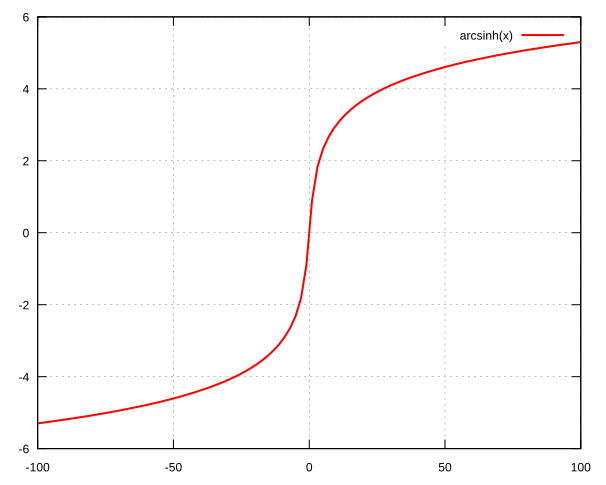
asinh

real theta = asinh(x);

\[\arcsinh(x) = \ln\left(x + \sqrt{x^2+1}\right)\]

Parameter:

x (real)

Output:

theta (real)

assert

Verify if a condition is true (same as C), if not the program stops.

assert(x==0)

Parameter:

Boolean condition

Output:

None

atan

\(\arctan\) function.

real theta = atan(x);

Parameter:

x (real)

Output:

theta (real)

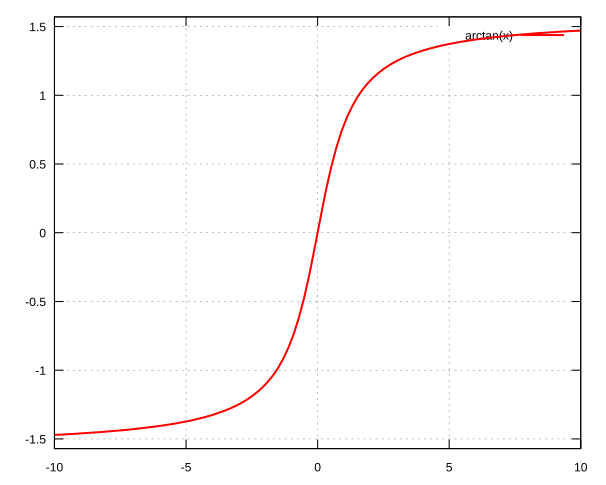
atan2

\(\displaystyle{\arctan\left(\frac{y}{x}\right)}\) function, returning the correct sign for \(\theta\).

real theta = atan2(y, x)

Parameter:

x (real)

Output:

theta (real)

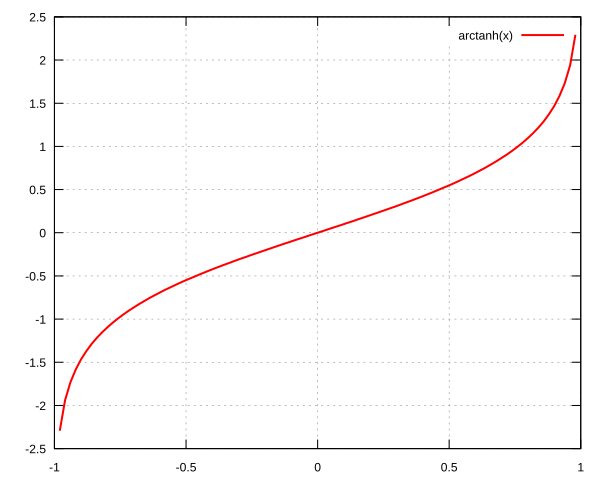
atanh

real theta = atanh(x);

Parameter:

x (real)

Output:

theta (real)

atoi

Convert a string to an interger.

int a = atoi(s);

Parameter:

s (string)

Output:

a (int)

atof

Convert a string to a real.

real a = atof(s);

Parameter:

s (string)

Output:

a (real)

BFGS

Todo

todo

buildmesh

Build a 2D mesh using border elements.

mesh Th = buildmesh(b1(nn) + b2(nn) + b3(nn) + b4(nn),[points=Points], ][nbvx=Nbvx], [fixedborder=FixedBorder]);

Parameters:

b1, b2, b3, b4 (border)

Geometry border, b1(nn) means b1 border discretized by nn vertices
points (real[int, int]) [Optional]

Specify a set of points

The size of Points array is (nbp, 2), containing a set of nbp points with x and y coordinates
nbvx= (int) [Optional]

Maximum number of vertices Default: 9000
fixedborder= (bool) [Optional]

If true, mesh generator cannot change the boundary mesh

Default: false

Output:

Th (mesh) Resulting mesh

ceil

Round fractions up of \(x\).

int c = ceil(x);

Parameter:

x (real)

Output:

c (int)

change

Change a property of a mesh.

int[int] L = [0, 1];
Thnew = change(Th, label=L);

Parameters:

Th (mesh) Original mesh
label= L (int[int]) Pair of old and new label
region= R (int[int]) Pair of old and new region
flabel= l (func int) Function of int given the new label
fregion= r (func int) Function of int given the new region

Output:

Thnew (mesh) Mesh with changed parameters

checkmovemesh

Check a movemesh without mesh generation.

real minT = checkmovemesh(Th, [Dx, Dy]);

Parameters:

Same as movemesh

Output:

minT (real) Minimum triangle area

chi

Characteristic function of a mesh.

int IsInMesh = chi(Th)(x, y);

Parameters:

Th (mesh or mesh3)
x (real) Position \(x\)
y (real) Position \(y\)

Output:

IsInMesh (int) 1 if \((x,y)\in\) Th 0 if \((x,y)\not\in\) Th

clock

Get the clock in second.

real t = clock();

Parameter:

None

Output:

t (real) Current CPU time

complexEigenValue

Same as EigenValue for complex problems.

conj

Caculate the conjuguate of a complex number.

complex C1 = 1 + 1i;
complex C2 = conj(C1);

Parameter:

C1 (complex) Complex number

Output:

C2 (complex) Conjuguate of C1

convect

Characteristics Galerkin method.

real cgm = convect([Ux, Uy], dt, c);
real cgm = convect([Ux, Uy, Uz], dt, c);

Compute \(c\circ \mathbf{X}\) with \(\mathbf{X}(\mathbf{x}) = \mathbf{x}_{\tau}\) and \(\mathbf{x}_{\tau}\) is the solution of:

\[\begin{split}\begin{array}{rcl} \dot{\mathbf{x}}_{\tau} &=& \mathbf{u}(\mathbf{x}_{\tau})\\ \mathbf{x}_{\tau} &=& \mathbf{x} \end{array}\end{split}\]

Parameters:

ux (fespace function) Velocity: \(x\) component
uy (fespace function) Velocity: \(y\) component
uz (fespace function) 3D only

Velocity: \(z\) component
dt (real) Time step
c (fespace function) Function to convect

Output:

cgm (real) Result

copysign

C++ copysign function.

real s = copysign(a, b);

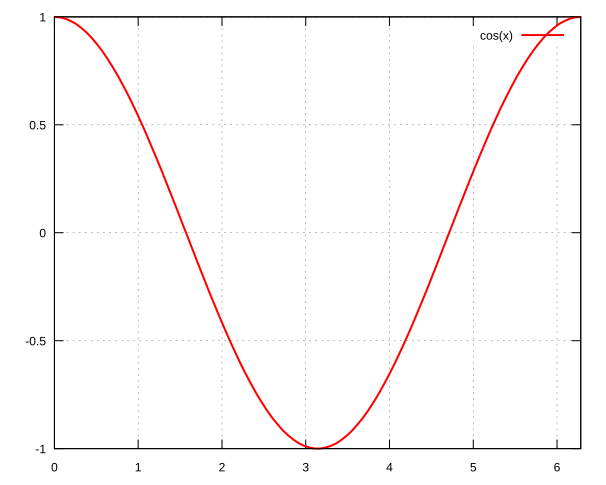
cos

\(\cos\) function.

real x = cos(theta);

Parameters:

theta (real or complex)

Output:

x (real or complex)

cosh

\(\cosh\) function.

real x = cosh(theta);

\[\cosh(x) = \frac{e^x + e^{-x}}{2}\]

Parameters:

theta (real)

Output:

x (real)

diffnp

Arithmetic useful function.

diffnp(a, b) = (a<0)&(0<b) ? (b-a) : 0;

diffpos

Arithmetic useful function.

diffpos(a, b) = max(b-a, 0);

dist

Arithmetic useful function.

dist(a, b) = sqrt(a^2 + b^2);
dist(a, b, c) = sqrt(a^2 + b^2 + c^2);

dumptable

Show all types, operators and functions in FreeFEM.

dumptable(out);

Parameters:

out (ostream) cout of ofstream file.

Output:

None

dx

\(x\) derivative.

Uh up = dx(u);

\[\frac{\partial u}{\partial x}\]

Parameters:

u (fespace function)

Output:

up (fespace function)

dxx

\(x\) double derivative.

Uh upp = dxx(u);

\[\frac{\partial^2 u}{\partial x^2}\]

Parameters:

u (fespace function)

Output:

upp (fespace function)

dxy

\(xy\) derivative.

Uh upp = dxy(u);

\[\frac{\partial^2 u}{\partial x\partial y}\]

Parameters:

u (fespace function)

Output:

upp (fespace function)

dxz

\(xz\) derivative.

Uh upp = dxz(u);

\[\frac{\partial^2 u}{\partial x\partial z}\]

Parameters:

u (fespace function)

Output:

upp (fespace function)

dy

\(y\) derivative.

Uh up = dy(u);

\[\frac{\partial u}{\partial y}\]

Parameters:

u (fespace function)

Output:

upp (fespace function)

dyx

\(yx\) derivative.

Uh upp = dyx(u);

\[\frac{\partial^2 u}{\partial y\partial x}\]

Parameters:

u (fespace function)

Output:

upp (fespace function)

dyy

\(y\) double derivative.

Uh upp = dyy(u);

\[\frac{\partial^2 u}{\partial x^2}\]

Parameters:

u (fespace function)

Output:

upp (fespace function)

dyz

\(yz\) derivative.

Uh upp = dyz(u);

\[\frac{\partial^2 u}{\partial y\partial z}\]

Parameters:

u (fespace function)

Output:

upp (fespace function)

dz

\(z\) derivative.

Uh up = dz(u);

\[\frac{\partial u}{\partial z}\]

Parameters:

u (fespace function)

Output:

upp (fespace function)

dzx

\(zx\) derivative.

Uh upp = dzx(u);

\[\frac{\partial^2 u}{\partial z\partial x}\]

Parameters:

u (fespace function)

Output:

upp (fespace function)

dzy

\(zy\) derivative.

Uh upp = dzy(u);

\[\frac{\partial^2 u}{\partial z\partial y}\]

Parameters:

u (fespace function)

Output:

upp (fespace function)

dzz

\(z\) double derivative.

Uh upp = dzz(u);

\[\frac{\partial^2 u}{\partial z^2}\]

Parameters:

u (fespace function)

Output:

upp (fespace function)

EigenValue

Compute the generalized eigenvalue of \(Au=\lambda Bu\). The shifted-inverse method is used by default with sigma=\(\sigma\), the shift of the method. The function EigenValue can be used for either matrices or functions returning a matrix vector product. The use of the matrix version is shown below.

int k = EigenValue(A,B,nev= , sigma= );

Parameters:

A, B: matrices of same size
nev=n: number of desired eigenvalues given by an integer n
sym=: the problem is symmetric or not
tol=: the relative accuracy to which eigenvalues are to be determined
value=: an array to store the real part of the eigenvalues
ivalue=: an array to store the imaginary part of the eigenvalues
vector=: a Finite Element function array to store the eigenvectors
sigma=: the shift value
Other parameters are available for more advanced use: see the ARPACK documentation.

Output: The output is the number of converged eigenvalues, which can be different than the number of requested eigenvalues given by nev=. Note that the eigenvalues and the eigenvectors are stored for further purposes using the parameters value= and vector=.

emptymesh

Build an empty mesh.

Useful to handle Lagrange multipliers in mixed and Mortar methods.

mesh eTh = emptymesh(Th, ssd);

Parameters:

Th (mesh) Mesh to empty
ssd (int[int]) Pseudo subregion label

Output:

eTh (mesh) Empty mesh

erf

The error function:

\[erf(x) = \frac{2}{\sqrt{pi}}\int_{0}^{x}{\exp(-t^2)dt}\]

real err = erf(x);

Parameters:

x (real)

Output:

err (real)

erfc

Complementary of the error function:

\[erfc(x) = 1-erf(x)\]

real errc = erfc(x);

Parameters:

x (real)

Output:

err (real)

exec

Execute an external command.

int v = exec(command);

Parameters:

command (string) Command to execute

Output:

v (int) Value returned by the command

exit

Exit function, equivalent to return.

exit(N);

Parameters:

N (int) Return value

Output:

None

exp

Exponential function.

real a = exp(b);

Parameters:

b (real or complex)

Output:

a (real or complex)

fdim

Positive difference (cmath function).

real fd = fdim(a, b);

Parameters:

a (real)
b (real)

Output:

fd (real) If \(x > y\), return \(x-y\)If \(x \leq y\), return \(0\)

floor

Floor function.

real a = floor(b);

Return the largest integer value not greater than b.

Parameters:

b (real)

Output:

a (real)

fmax

Maximum (cmath function).

real Max = fmax(a, b);

Parameters:

a (real)
b (real)

Output:

Max (real)

fmin

Minimum (cmath function).

real Min = fmin(a, b);

Parameters:

a (real)
b (real)

Output:

Min (real)

fmod

Remainder of \(a/b\) (cmath function).

real Mod = fmod(a, b);

Parameters:

a (real)
b (real)

Output:

Mod (real)

imag

Imaginary part of a complex number.

complex c = 1. + 1i;
real Im = imag(c);

int1d

1D integral.

int1d(Th, [Label], [qfe=Qfe], [qforder=Qforder])(
    ...
)

Used in problem, solve or varf definition to impose a boundary condition only (FreeFEM does not support 1D simulation), or outside to calculate a quantity.

Parameters:

Th (mesh) Mesh where the integral is calculated
Label (int) [Optional]

Label of the 1D border Default: all borders of the mesh
qfe= (quadrature formula) [Optional] (qf3E by default)

Quadrature formula, see quadrature formulae
qforder= (quadrature formula) [Optional]

Quadrature order, see quadrature formulae

Output:

Depending on the situation: In a problem, solve or varf definition: Non relevant.

Outside: real (example: real l = int1d(Th, 1)(1.);).

Warning

In a problem, solve or varf definition, the content of int1d must be a linear or bilinear form.

int2d

2D integral.

int2d(Th, [Region], [qft=Qft], [qforder=Qforder])(
    ...
)

int2d(Th, [Label], [qft=Qft], [qforder=Qforder])(
    ...
)

Used in problem, solve or varf definition to: - Calculate integral in 2D simulation - Impose a boundary condition in 3D simulation Or outside to calculate a quantity.

Parameters:

Th (mesh, mesh3 , meshS`or :freefem:`meshL) Mesh where the integral is calculated
Region (int) [Optional] Label of the 2D region (2D simulation or Surface simulation) Default: all regions of the mesh
Label (int) [Optional] Label of the 2D border (3D simulation) Default: all borders of the mesh
qft= (quadrature formula) [Optional] (qf5T by default)

Quadrature formula, see quadrature formulae
qforder= (quadrature formula) [Optional]

Quadrature order, see quadrature formulae

Output:

Depending on the situation: In a problem, solve or varf definition: Non relevant. Outside: real (example: real s = int2d(Th, 1)(1.);).

Warning

In a problem, solve or varf definition, the content of the int2d must be a linear or bilinear form.

int3d

3D integral.

int3d(Th, [Region], [qfV=QfV], [qforder=Qforder])(
    ...
)

Used in problem, solve or varf definition to calculate integral in 3D simulation, or outside to calculate a quantity.

Parameters:

Th (mesh3) Mesh where the integral is calculated
Region (int) [Optional]

Label of the 3D region

Default: all regions of the mesh
qfV= (quadrature formula) [Optional] (qf5V by default)

Quadrature formula, see quadrature formulae
qforder= (quadrature formula) [Optional]

Quadrature order, see quadrature formulae

Output:

Depending on the situation: In a problem, solve or varf definition: Non relevant. Outside: real (example: real v = int3d(Th, 1)(1.);).

Warning

In a problem, solve or varf definition, the content of the int3d must be a linear or bilinear form.

intalledges

Integral on all edges.

intalledges(Th, [Region])(
    ...
)

Parameters:

Th (mesh) Mesh where the integral is calculated
Region (int) [Optional]

Label of the region

Default: all regions of the mesh

Output:

Non relevant

intallfaces

Intergal on all faces.

Same as intalledges for mesh3.

interpolate

Interpolation operator from a finite element space to another.

matrix I = interpolate(Wh, Vh, [inside=Inside], [t=T], [op=Op], [U2Vc=U2VC]);

Parameters:

Wh (fespace) Target finite element space
Vh (fespace) Original finite element space
inside= (bool) If true, create a zero extension outside the Vh domain
t= (bool) If true, return the transposed matrix
op= (int) 0: interpolate the function (default value) 1: interpolate \(\partial_x\) 2: interpolate \(\partial_y\) 3: interpolate \(\partial_z\)
U2Vc= (int[int]) Array of the same size of Wh describing which component of Vhis interpolated in Wh

Output:

I (matrix) Interpolation matrix operator

invdiff

Arithmetic useful function.

invdiff(a, b) = (abs(a-b) < 10^(-30)) ? (a-b) : 1/(a-b)
invdiff(a, b, e) = (abs(a-b) < e) ? (a-b) : 1/(a-b)

invdiffnp

Arithmetic useful function.

invdiffnp(a, b) = (a<0)&(0<b) ? 1/(b-a) : 0

invdiffpos

Arithmetic useful function.

invdiffpos(a, b) = (a<b) ? 1./(b-a) : 0

isInf

The C++ isInf function.

bool b = isInf(a);

isNaN

The C++ isNan function.

bool b = isNaN(a);

isNormal

The C++ isNormal function.

j0

Bessel function of first kind, order 0.

real b = j0(x);

Parameters:

x (real)

Output:

b (real)

j1

Bessel function of first kind, order 1.

real b = j1(x);

Parameters:

x (real)

Output:

b (real)

jn

Bessel function of first kind, order n.

real b = jn(n, x);

\[J_n(x) = \sum_{p=0}^{\infty}\frac{(1)^p}{p!(n+p)!}\left(\frac{x}{2}\right)^{2p+n}\]

Parameters:

n (int)
x (real)

Output:

b (real)

jump

Jump function across an edge.

intalledges(
    ... jump(c) ...
)

Parameters:

c (fespace function) Discontinuous function

Output:

Non relevant

LinearCG

Linear CG solver

Parameters and output are the same as AffineCG

LinearGMRES

Linear GMRES solver

Parameters and output are the same as AffineCG

lgamma

Natural logarithm of the absolute value of the \(\Gamma\) function of \(x\).

real lg = lgamma(x);

Parameters:

x (real)

Output:

lg (real)

log

Natural logarithm.

real l = log(x);

Parameters:

x (real or complex)

Output:

l (real or complex)

Note

Complex value

For complex value, the log function is defined as:

\[\log(z) = \log(|z|) + i\arg(z)\]

log10

Common logarithm.

real l = log10(x);

Parameters:

x (real)

Output:

l (real)

lrint

Integer value nearest to \(x\).

int l = lrint(a);

Parameters:

a (real)

Output:

l (int)

lround

Round a value, and return an integer value.

int l = lround(a);

Parameters:

a (real)

Output:

l (int)

ltime

Return the current time since the Epcoh.

int t = ltime();

Parameter:

None

Output:

t (int)

max

Maximum value of two, three or four values.

real m = max(a, b);
real m = max(a, b, c);
real m = max(a, b, c, d);

Parameters:

a (int or real)
b (int or real)
c (int or real) [Optional]
d (int or real) [Optional]

Output:

b (int or real)

min

Minimum value of two, three or four values.

real m = min(a, b);
real m = min(a, b, c);
real m = min(a, b, c, d);

Parameters:

a (int or real)
b (int or real)
c (int or real) [Optional]
d (int or real) [Optional]

Output:

b (int or real)

movemesh

Move a mesh.

mesh MovedTh = movemesh(Th, [Dx, Dy]);
mesh3 MovedTh = movemesh(Th, [Dx, Dy, Dz], [region=Region], [label=Label], [facemerge=FaceMerge], [ptmerge=PtMerge], [orientation=Orientation]);

Parameters:

Th (mesh of mesh3) Mesh to move
Dx (fespace function) Displacement along \(x\)
Dy (fespace function) Displacement along \(y\)
Dz (fespace function) 3D only

Displacement along \(z\)
region= (int) [Optional] 3D only

Set label to tetrahedra
label= (int[int]) [Optional] 3D only

Set label of faces (see change for more information)
facemerge= (int) [Optional] 3D only

If equal to 1, some faces can be merged during the mesh moving Default: 1
ptmerge= (real) [Optional] 3D only

Criteria to define when two points merge
orientation= (int) [Optional] 3D only

If equal to 1, allow orientation reverse if tetrahedra is not positive Default: 1

Output:

MovedTh (mesh or mesh3) Moved mesh

NaN

C++ nan function.

real n = NaN([String]);

Parameters:

String (string) Default: ""

NLCG

Non-linear conjugate gradient.

Parameters and output are the same as AffineCG

on

Dirichlet condition function.

problem (u, v)
    ...
    + on(Label, u=uD)
    ...

Warning

Used only in problem, solve and varf

Parameters:

Label (int or border in 2D)

Boundary reference where to impose the Dirichlet condition
uD (fespace function, func or real or int)

Dirichlet condition (u is an unknown of the problem)

Output:

Non relevant

plot

Plot meshes and results.

plot([Th], [u], [[Ux, Uy, Uz]], [wait=Wait], [ps=PS], [coef=Coef], [fill=Fill], cmm=[Cmm], [value=Value], [aspectratio=AspectRatio], [bb=Bb], [nbiso=NbIso], [nbarrow=NbArrow], [viso=VIso], [varrow=VArrow], [bw=Bw], [grey=Grey], [hsv=Hsv], [boundary=Boundary], [dim=Dim], [prev=Prev], [WindowIndex=WI]);

Note

Only one of Th, u or [Ux, Uy] / [Ux, Uy, Uz] is needed for the plot command.

Parameters:

Th (mesh or mesh3) Mesh to display
u (fespace function) Scalar fespace function to display
[Ux, Uy] / [Ux, Uy, Uz] (fespace function array) Vectorial fespace function to display
[Ux, Uy] ([real[int], real[int]]) Couple a real array to display a curve
wait= (bool) If true, wait before continue
ps= (string) Name of the file to save the plot (.ps or .eps format)
coef= (real) Arrow size
fill= (bool) If true, fill color between isovalue (usable with scalar fespace function only)
cmm= (string) Text comment in the graphic window
value= (bool) If true, show the value scale
aspectratio= (bool) If true, preserve the aspect ratio
bb= ([real[int], real[int]]) Specify a bounding box using two corner points
nbiso= (int) Number of isovalues
nbarrow= (int) Number of colors of arrows values
viso= (real[int]) Specify an array of isovalues
varrow= (real[int]) Specify an array of arrows values color
bw= (bool) If true, the plot is in black and white
grey= (bool) If true, the plot is in grey scale
hsv= (real[int]) Array of \(3\times n\) values defining HSV color model \([h_1, s_1, v_1, ..., h_n, s_n, v_n]\)
boundary= (bool) If true, display the boundary of the domain
dim= (int) Set the dimension of the plot: 2 or 3
prev= (bool) Use the graphic state of the previous state
WindowIndex= (int) Specify window index for multiple windows graphics

Output:

None

See the plot section for in-graphic commands.

polar

Polar coordinates.

complex p = polar(a, b);

Parameters:

a (real)
b (real)

Output:

p (complex)

pow

Power function.

real p = pow(a, b);

\(p=a^b\)

Parameters:

a (real)
b (real)

Output:

p (real)

projection

Arithmetic useful function.

real p = projection(a, b, x);

Projection is equivalent to:

projection(a, b, x) = min(max(a, x), b)*(a < b) + min(max(b, x), a)*(1-(a < b));

Parameters:

a (real)
b (real)
x (real)

Output:

p (real)

randinit

Initialize the state vector by using a seed.

randinit(seed);

Parameters:

seed (int)

Output:

None

randint31

Generate unsigned int (31 bits) random number.

int r = randint31();

Parameters:

None

Output:

r (int)

randint32

Generate unsigned int (32 bits) random number.

int r = randint32();

Parameters:

None

Output:

r (int)

randreal1

Generate uniform real in \([0, 1]\) (32 bits).

real r = randreal1();

Parameters:

None

Output:

r (real)

randreal2

Generate uniform real in \([0, 1)\) (32 bits).

real r = randreal2();

Parameters:

None

Output:

r (real)

randreal3

Generate uniform real in \((0, 1)\) (32 bits).

real r = randreal3();

Parameters:

None

Output:

r (real)

randres53

Generate uniform real in \([0, 1)\) (53 bits).

real r = randres53();

Parameters:

None

Output:

r (real)

readmesh

Read a 2D mesh file at different formats (see Mesh Generation).

mesh Th = readmesh(MeshFileName);

Parameters:

MeshFileName (string)

Output:

Th (mesh)

readmesh3

Read a 3D mesh file at different formats (see Mesh Generation).

mesh3 Th = readmesh3(MeshFileName);

Parameters:

MeshFileName (string)

Output:

Th (mesh3)

real

Return the real part of a complex number.

real r = real(c);

Parameters:

c (complex)

Output:

r (real)

rint

Integer value nearest to \(x\) (real value).

real r = rint(a);

Parameters:

a (real)

Output:

r (real)

round

Round a value (real value).

real r = round(a);

Parameters:

a (real)

Output:

r (real)

savemesh

Save a 2D or 3D mesh in different formats (see Mesh Generation 2D and Mesh Generation 3D).

savemesh(Th, MeshFileName);

Parameters:

Th (mesh or mesh3)
MeshFileName (string)

Output:

None

set

Set a property to a matrix. See matrix.

sign

Sign of a value.

int s = sign(a);

Parameters:

a (real or int)

Output:

s (int)

signbit

C++ signbit function

int s = signbit(a);

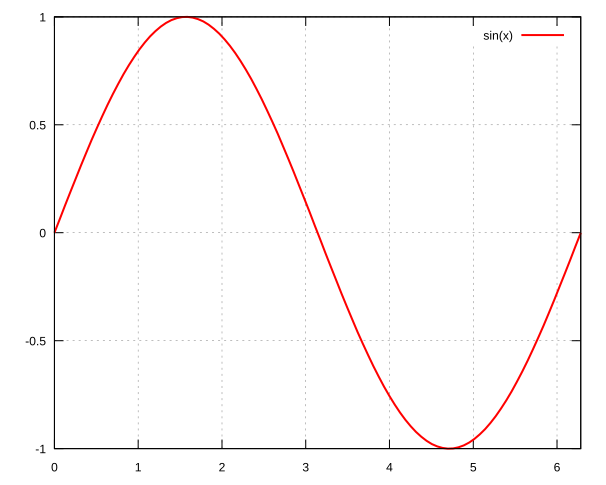
sin

\(\sin\) function.

real x = sin(theta);

Parameter:

theta (real or complex)

Output:

x (real or complex)

sinh

\(\sinh\) function.

real x = sinh(theta);

\[\sinh(x) = \frac{e^{x} - e^{-x}}{2}\]

Parameter:

theta (real)

Output:

x (real)

sort

Sort two array in parallel

sort(A, B);

Parameters:

A (real[int])
B (int[int])

Output:

None

A is sorted in ascending order, B is sorted as A.

splitmesh

Split mesh triangles according to a function.

Th = splitmesh(Th0, f);

Parameters:

Th0 (mesh)
f (func or fespace function)

Output:

Th (mesh)

sqrt

Square root

real s = sqrt(a);

Parameter:

a (real)

Output:

s (real)

square

Square of a number.

real S = square(a);

Parameter:

a (real)

Output:

S (real)

Build a structured square mesh.

mesh Th = square(nnX, nnY, [[L*x, H*y]], [flags=Flags], [label=Labels], [region=Region]);

Parameters:

nnX (int) Discretization along \(x\)
nnY (int) Discretization along \(y\)
L (real) [Optional] Length along \(x\)
H (real) [Optional] Height along \(y\)
flags= (int) [Optional]
label= (int[int]) [Optional]
region= (int) [Optional]

Structured mesh type, see Mesh Generation chapter for more information

Output:

Th (mesh)

storagetotal

int total = storagetotal();

storageused

int used = storageused();

strtod

C++ strtod function

string text = "10.5";
real number = strtod(text);

Parameter:

text (string)

Output:

number (real)

strtol

C++ strtol function

string text = "10";
int number = strtol(text);

int base = 16;
int number = strtol(text, base);

Parameter:

text (string)
base (int) Base [Optional]

Output:

number (int)

swap

Swap values.

swap(a, b);

Parameters:

a (real)
b (real)

Output:

None

system

Execute a system command.

int Res = system(Command);

Parameter:

Command (string) System command

Output:

Res (int) Value returned by the system command

Note

On Windows, the full path of the command is needed. For example, to execute ls.exe:

int Res = exec("C:\\cygwin\\bin\\ls.exe");

tan

\(\tan\) function.

real x = tan(theta);

Parameter:

theta (real)

Output:

x (real)

tanh

\(\tanh\) function.

real x = tanh(theta);

Parameter:

theta (real)

Output:

x (real)

tgamma

Calculate the \(\Gamma\) function of \(x\).

real tg = tgamma(x);

Parameter:

x (real)

Output:

tg (real)

time

Return the current time (C++ function).

real t = time();

Parameter:

None

Output:

t (real)

trace

Matrix trace

real tr = trace([[1, 2], [3, 4]]);

Parameters:

Matrix

Output:

Trace of the matrix (real)

trunc

Split triangle of a mesh.

mesh Th = trunc(Th0, R, [split=Split], [label=Label]);

Parameters:

Th0 (mesh)
R (bool or int) Split triangles where R is true or different from 0
split= (int) [Optional]

Level of splitting Default: 1
label= (int) [Optional]

Label number of new boundary item Default: 1

Output:

Th (mesh)

y0

Bessel function of second kind, order 0.

real B = y0(x);

Parameters:

x (real)

Output:

b (real)

y1

Bessel function of second kind, order 1.

real B = y1(x);

Parameters:

x (real)

Output:

b (real)

yn

Bessel function of second kind, order n.

real B = yn(n, x);

\[Y_n(x) = \lim_{\lambda\rightarrow n}{\frac{J_{\lambda}(x)\cos(\lambda\pi)-J_{-\lambda}(x)}{\sin(\lambda\pi)}}\]

Parameters:

n (int)
x (real)

Output:

b (real)

Here you can use the search bar to search in all FreeFEM examples instead

The list of all matching examples on the right is updated for each new query

Clicking on a search hit or on an example on the right brings up the corresponding script from GitHub

You can also filter the list on the right by selecting one or more intersecting categories on the left tree

Functions

abs

acos

acosh

adaptmesh

adj

AffineCG

AffineGMRES

arg

asin

asinh

assert

atan

atan2

atanh

atoi

atof

BFGS

buildmesh

ceil

change

checkmovemesh

chi

clock

complexEigenValue

conj

convect

copysign

cos

cosh

diffnp

diffpos

dist

dumptable

dx

dxx

dxy

dxz

dy

dyx

dyy

dyz

dz

dzx

dzy

dzz

EigenValue

emptymesh

erf

erfc

exec

exit

exp

fdim

floor

fmax

fmin

fmod

imag

int1d

int2d

int3d

intalledges

intallfaces

interpolate

invdiff

invdiffnp

invdiffpos

isInf

isNaN

isNormal

j0

j1

jn

jump

LinearCG