The System of elasticity

Elasticity

Solid objects deform under the action of applied forces:

a point in the solid, originally at \((x,y,z)\) will come to \((X,Y,Z)\) after some time; the vector \(\mathbf{u}=(u_1,u_2,u_3) = (X-x, Y-y, Z-z)\) is called the displacement. When the displacement is small and the solid is elastic, Hooke’s law gives a relationship between the stress tensor \(\sigma(u)=(\sigma_{ij}(u) )\) and the strain tensor \(\epsilon(u)=\epsilon_{ij}(u)\)

\[\sigma_{ij}(u) = \lambda \delta_{ij} \nabla.\mathbf{u}+ 2\mu\epsilon_{ij}(u),\]

where the Kronecker symbol \(\delta_{ij} = 1\) if \(i=j\), \(0\) otherwise, with

\[\epsilon_{ij}(u) = {1\over 2}({\partial u_i\over\partial x_j} + {\partial u_j\over\partial x_i} ),\]

and where \(\lambda, \mu\) are two constants that describe the mechanical properties of the solid, and are themselves related to the better known constants \(E\), Young’s modulus, and \(\nu\), Poisson’s ratio:

\[\mu = {E\over 2( 1+\nu)}, \quad \lambda = {E\nu\over (1+\nu)(1-2\nu)}.\]

Lamé’s system

Let us consider a beam with axis \(Oz\) and with perpendicular section \(\Omega\). The components along \(x\) and \(y\) of the strain \({\bf u}(x)\) in a section \(\Omega\) subject to forces \({\bf f}\) perpendicular to the axis are governed by:

\[-\mu \Delta {\bf u} - (\mu+\lambda) \nabla (\nabla .{\bf u})={\bf f}~~\hbox{in}~~\Omega,\]

where \(\lambda\) ,\(\mu\) are the Lamé coefficients introduced above.

Remark, we do not use this equation because the associated variational form does not give the right boundary condition, we simply use:

\[- div( \sigma ) = \mathbf{f} \quad \mbox{in}~~\Omega\]

where the corresponding variational form is:

\[\int_{\Omega} \sigma(u) : \epsilon(\mathbf{v})\;dx - \int_{\Omega} \mathbf{v} f \;dx =0;\]

where \(:\) denotes the tensor scalar product, i.e. \(a: b = \sum_{i,j} a_{ij}b_{ij}\).

So the variational form can be written as :

\[\int_{\Omega} \lambda \nabla.u \nabla.v + 2 \mu \epsilon(\mathbf{u}):\epsilon(\mathbf{v}) \; dx - \int_{\Omega} \mathbf{v} f \;dx =0;\]

Tip

Consider an elastic plate with the undeformed rectangle shape \([0,20]\times [-1,1]\).

The body force is the gravity force \(\mathbf{f}\) and the boundary force \(\mathbf{g}\) is zero on lower, upper and right sides. The left vertical side of the beam is fixed. The boundary conditions are:

\[\begin{split}\begin{array}{rcll} \sigma . {\bf n} &= \mathbf{g} &= 0 & \hbox{ on }\Gamma_1, \Gamma_4, \Gamma_3, \\ {\bf u} &= \mathbf{0} && \hbox{ on }\Gamma_2 \end{array}\end{split}\]

Here \({\bf u}=(u,v)\) has two components.

The above two equations are strongly coupled by their mixed derivatives, and thus any iterative solution on each of the components is risky. One should rather use FreeFEM’s system approach and write:

// Parameters
real E = 21e5;
real nu = 0.28;

real f = -1;

// Mesh
mesh Th = square(10, 10, [20*x,2*y-1]);

// Fespace
fespace Vh(Th, P2);
Vh u, v;
Vh uu, vv;

// Macro
real sqrt2=sqrt(2.);
macro epsilon(u1,u2) [dx(u1),dy(u2),(dy(u1)+dx(u2))/sqrt2] //
// The sqrt2 is because we want: epsilon(u1,u2)'* epsilon(v1,v2) = epsilon(u): epsilon(v)
macro div(u,v) ( dx(u)+dy(v) ) //

// Problem
real mu= E/(2*(1+nu));
real lambda = E*nu/((1+nu)*(1-2*nu));

solve lame([u, v], [uu, vv])
   = int2d(Th)(
        lambda * div(u, v) * div(uu, vv)
      + 2.*mu * ( epsilon(u,v)' * epsilon(uu,vv) )
   )
   - int2d(Th)(
        f*vv
   )
   + on(4, u=0, v=0)
   ;

// Plot
real coef=100;
plot([u, v], wait=1, ps="lamevect.eps", coef=coef);

// Move mesh
mesh th1 = movemesh(Th, [x+u*coef, y+v*coef]);
plot(th1,wait=1,ps="lamedeform.eps");

// Output
real dxmin = u[].min;
real dymin = v[].min;

cout << " - dep. max x = "<< dxmin << " y=" << dymin << endl;
cout << "   dep. (20, 0) = " << u(20, 0) << " " << v(20, 0) << endl;

The output is:

-- square mesh : nb vertices  =121 ,  nb triangles = 200 ,  nb boundary edges 40
-- Solve :           min -0.00174137  max 0.00174105
         min -0.0263154  max 1.47016e-29
- dep.  max   x = -0.00174137 y=-0.0263154
   dep.  (20,0)  = -1.8096e-07 -0.0263154
times: compile 0.010219s, execution 1.5827s

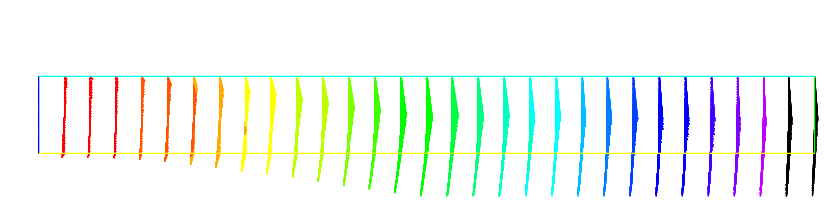
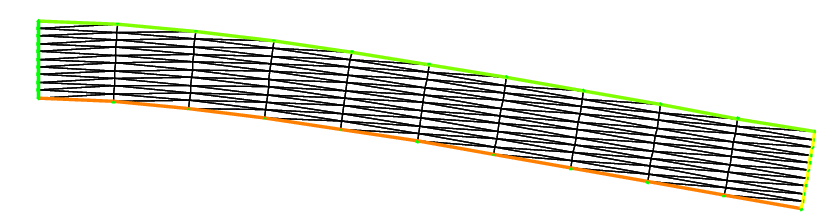
Solution of Lamé’s equations for elasticity for a 2D beam deflected by its own weight and clamped by its left vertical side is shown Fig. 19 and Fig. 20. Result are shown with a amplification factor equal to 100. The size of the arrow is automatically bound, but the color gives the real length.

Elasticity

Here you can use the search bar to search in all FreeFEM examples instead

The list of all matching examples on the right is updated for each new query

Clicking on a search hit or on an example on the right brings up the corresponding script from GitHub

You can also filter the list on the right by selecting one or more intersecting categories on the left tree

The System of elasticity