Domain decomposition

We present three classic examples of domain decomposition technique: first, Schwarz algorithm with overlapping, second Schwarz algorithm without overlapping (also call Shur complement), and last we show to use the conjugate gradient to solve the boundary problem of the Shur complement.

Schwarz overlapping

To solve:

\[-\Delta u =f,\;\mbox{in}\;\Omega=\Omega_1\cup\Omega_2\quad u|_\Gamma=0\]

the Schwarz algorithm runs like this:

\[\begin{split}\begin{array}{rcl} -\Delta u^{n+1}_1&=&f\;\mbox{in}\;\Omega_1\quad u^{n+1}_1|_{\Gamma_1}=u^n_2\\ -\Delta u^{n+1}_2&=&f\;\mbox{in}\;\Omega_2\quad u^{n+1}_2|_{\Gamma_2}=u^n_1 \end{array}\end{split}\]

where \(\Gamma_i\) is the boundary of \(\Omega_i\) and on the condition that \(\Omega_1\cap\Omega_2\neq\emptyset\) and that \(u_i\) are zero at iteration 1.

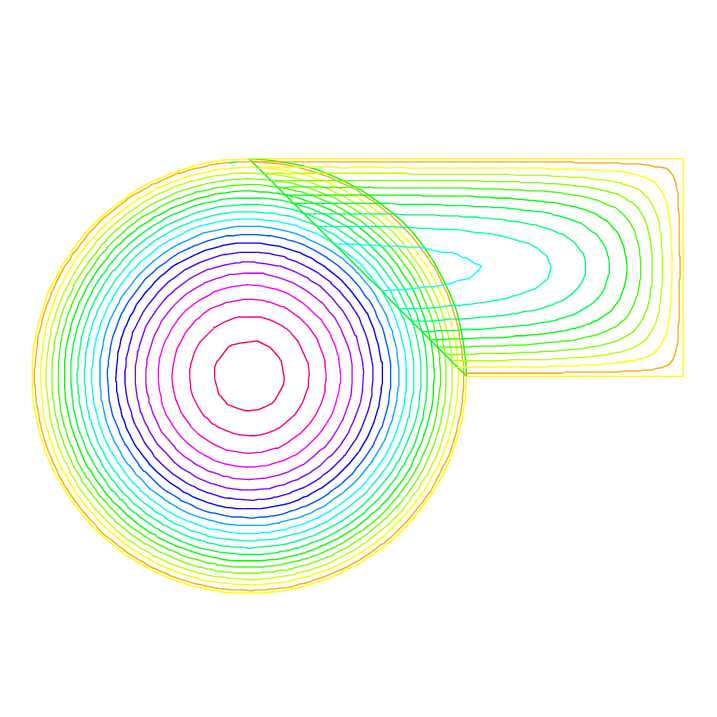
Here we take \(\Omega_1\) to be a quadrangle, \(\Omega_2\) a disk and we apply the algorithm starting from zero.

Fig. 165 The 2 overlapping mesh TH and th

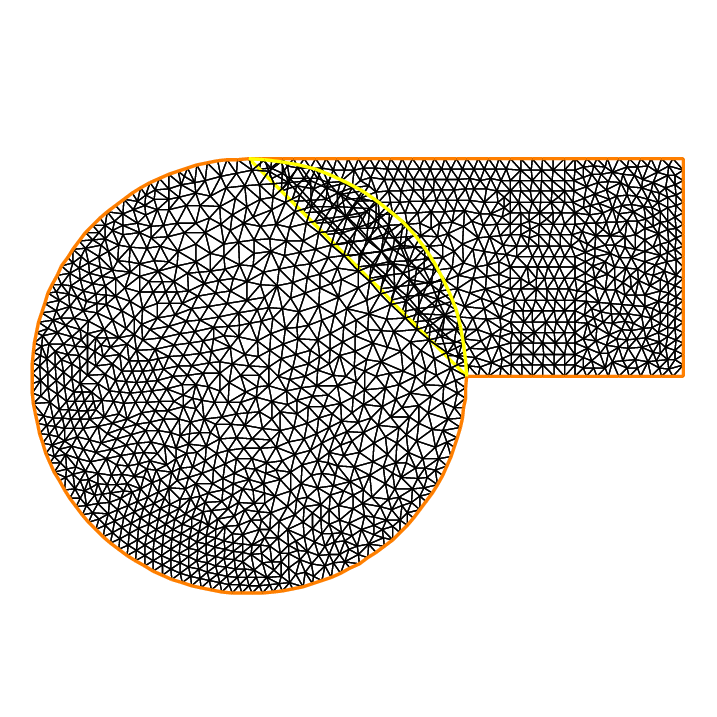
Tip

Schwarz overlapping

// Parameters
int inside =2; //inside boundary
int outside = 1; //outside boundary
int n = 4;

// Mesh
border a(t=1, 2){x=t; y=0; label=outside;}
border b(t=0, 1){x=2; y=t; label=outside;}
border c(t=2, 0){x=t; y=1; label=outside;}
border d(t=1, 0){x=1-t; y=t; label=inside;}
border e(t=0, pi/2){x=cos(t); y=sin(t); label=inside;}
border e1(t=pi/2, 2*pi){x=cos(t); y=sin(t); label=outside;}
mesh th = buildmesh(a(5*n) + b(5*n) + c(10*n) + d(5*n));
mesh TH = buildmesh(e(5*n) + e1(25*n));
plot(th, TH, wait=true); //to see the 2 meshes

// Fespace
fespace vh(th, P1);
vh u=0, v;

fespace VH(TH, P1);
VH U, V;

// Problem
int i = 0;
problem PB (U, V, init=i, solver=Cholesky)
   = int2d(TH)(
         dx(U)*dx(V)
       + dy(U)*dy(V)
   )
   + int2d(TH)(
       - V
   )
   + on(inside, U=u)
   + on(outside, U=0)
   ;

problem pb (u, v, init=i, solver=Cholesky)
   = int2d(th)(
         dx(u)*dx(v)
       + dy(u)*dy(v)
   )
   + int2d(th)(
       - v
   )
   + on(inside, u=U)
   + on(outside, u=0)
   ;

// Calculation loop
for (i = 0 ; i < 10; i++){
   // Solve
   PB;
   pb;

   // Plot
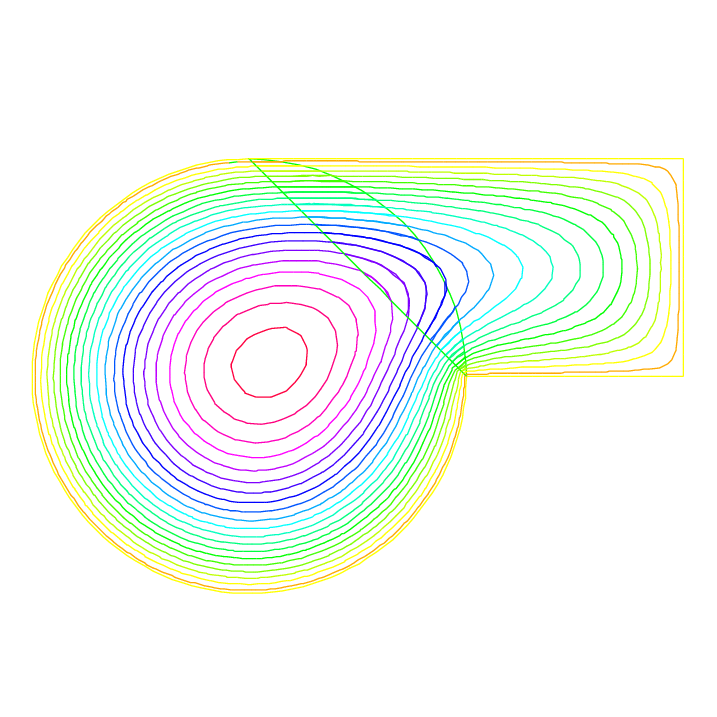
   plot(U, u, wait=true);
}

Fig. 166 Isovalues of the solution at iteration 0

Fig. 167 Isovalues of the solution at iteration 0

Schwarz overlapping

Schwarz non overlapping Scheme

To solve:

\[-\Delta u =f\;\mbox{in}\;\Omega=\Omega_1\cup\Omega_2\quad u|_\Gamma=0\]

the Schwarz algorithm for domain decomposition without overlapping runs like this

Fig. 168 The two none overlapping mesh TH and th

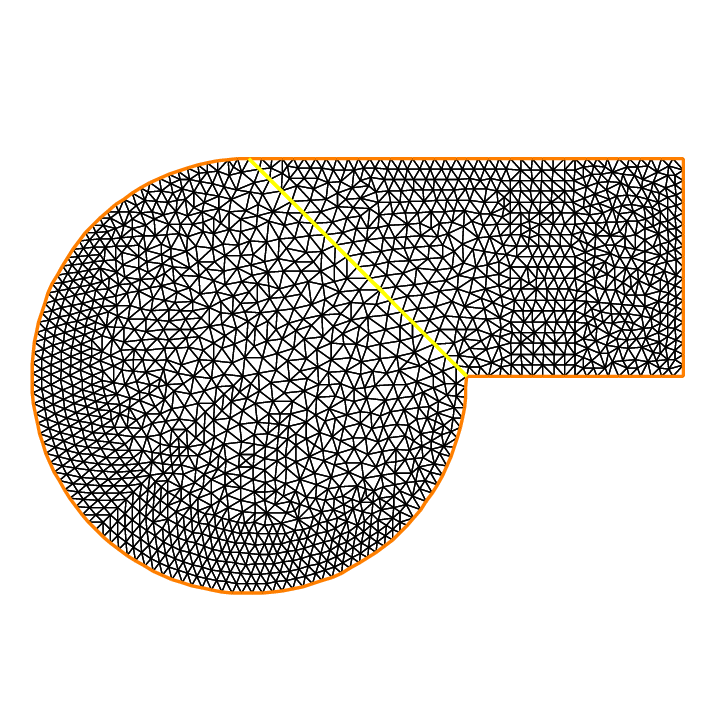
Let introduce \(\Gamma_i\) is common the boundary of \(\Omega_1\) and \(\Omega_2\) and \(\Gamma_e^i= \partial \Omega_i \setminus \Gamma_i\).

The problem find \(\lambda\) such that \((u_1|_{\Gamma_i}=u_2|_{\Gamma_i})\) where \(u_i\) is solution of the following Laplace problem:

\[-\Delta u_i=f\;\mbox{in}\;\Omega_i\quad u_i|_{\Gamma_i}=\lambda \quad u_i|_{\Gamma_e^i} = 0\]

To solve this problem we just make a loop with upgrading \(\lambda\) with

\[\lambda = \lambda {\pm} \frac{(u_1-u_2)}{2}\]

where the sign \(+\) or \(-\) of \({\pm}\) is choose to have convergence.

Tip

Schwarz non-overlapping

// Parameters
int inside = 2; int outside = 1; int n = 4;

// Mesh
border a(t=1, 2){x=t; y=0; label=outside;};
border b(t=0, 1){x=2; y=t; label=outside;};
border c(t=2, 0){x=t; y=1; label=outside;};
border d(t=1, 0){x=1-t; y=t; label=inside;};
border e(t=0, 1){x=1-t; y=t; label=inside;};
border e1(t=pi/2, 2*pi){x=cos(t); y=sin(t); label=outside;};
mesh th = buildmesh(a(5*n) + b(5*n) + c(10*n) + d(5*n));
mesh TH = buildmesh(e(5*n) + e1(25*n));
plot(th, TH, wait=true);

// Fespace
fespace vh(th, P1);
vh u=0, v;
vh lambda=0;

fespace VH(TH, P1);
VH U, V;

// Problem
int i = 0;
problem PB (U, V, init=i, solver=Cholesky)
    = int2d(TH)(
          dx(U)*dx(V)
        + dy(U)*dy(V)
    )
    + int2d(TH)(
        - V
    )
    + int1d(TH, inside)(
          lambda*V
    )
    + on(outside, U= 0 )
    ;

problem pb (u, v, init=i, solver=Cholesky)
    = int2d(th)(
          dx(u)*dx(v)
        + dy(u)*dy(v)
    )
    + int2d(th)(
        - v
    )
    + int1d(th, inside)(
        - lambda*v
    )
    + on(outside, u=0)
    ;

for (i = 0; i < 10; i++){
    // Solve
    PB;
    pb;
    lambda = lambda - (u-U)/2;

    // Plot
    plot(U,u,wait=true);
}

// Plot
plot(U, u);

Fig. 169 Isovalues of the solution at iteration 0 without overlapping

Fig. 170 Isovalues of the solution at iteration 9 without overlapping

Schwarz conjuguate gradient

To solve \(-\Delta u =f \;\mbox{in}\;\Omega=\Omega_1\cup\Omega_2\quad u|_\Gamma=0\) the Schwarz algorithm for domain decomposition without overlapping runs like this

Let introduce \(\Gamma_i\) is common the boundary of \(\Omega_1\) and \(\Omega_2\) and \(\Gamma_e^i= \partial \Omega_i \setminus \Gamma_i\).

The problem find \(\lambda\) such that \((u_1|_{\Gamma_i}=u_2|_{\Gamma_i})\) where \(u_i\) is solution of the following Laplace problem:

\[-\Delta u_i=f\;\mbox{in}\;\Omega_i\quad u_i|_{\Gamma_i}=\lambda \quad u_i|_{\Gamma_e^i} = 0\]

The version of this example uses the Shur complement. The problem on the border is solved by a conjugate gradient method.

Tip

Schwarz conjugate gradient

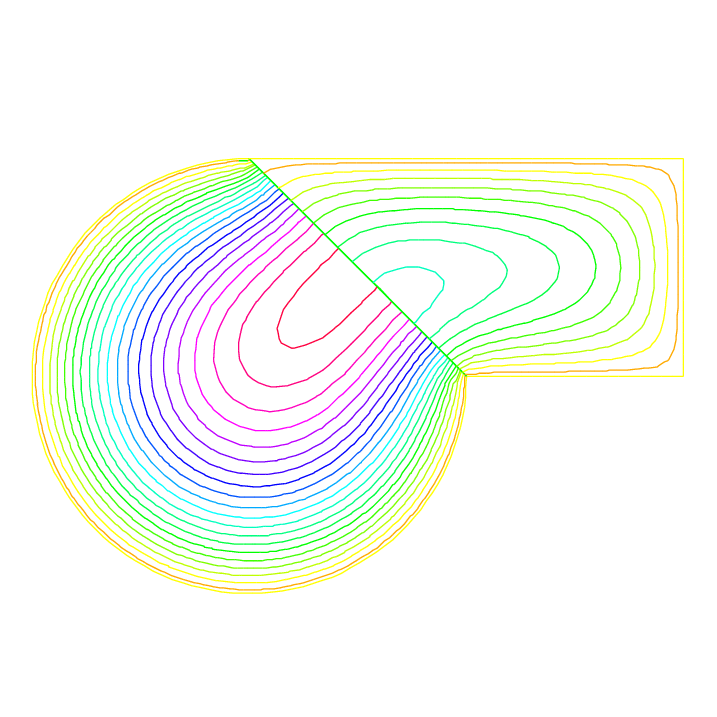
First, we construct the two domains:

// Parameters
int inside = 2; int outside = 1; int n = 4;

// Mesh
border Gamma1(t=1, 2){x=t; y=0; label=outside;}
border Gamma2(t=0, 1){x=2; y=t; label=outside;}
border Gamma3(t=2, 0){x=t; y=1; label=outside;}
border GammaInside(t=1, 0){x=1-t; y=t; label=inside;}
border GammaArc(t=pi/2, 2*pi){x=cos(t); y=sin(t); label=outside;}
mesh Th1 = buildmesh(Gamma1(5*n) + Gamma2(5*n) + GammaInside(5*n) + Gamma3(5*n));
mesh Th2 = buildmesh(GammaInside(-5*n) + GammaArc(25*n));
plot(Th1, Th2);

Now, define the finite element spaces:

// Fespace
fespace Vh1(Th1, P1);
Vh1 u1, v1;
Vh1 lambda;
Vh1 p=0;

fespace Vh2(Th2,P1);
Vh2 u2, v2;

Note

It is impossible to define a function just on a part of boundary, so the \(\lambda\) function must be defined on the all domain \(\Omega_1\) such as:

Vh1 lambda;

The two Poisson’s problems:

problem Pb1 (u1, v1, init=i, solver=Cholesky)
    = int2d(Th1)(
          dx(u1)*dx(v1)
        + dy(u1)*dy(v1)
    )
    + int2d(Th1)(
        - v1
    )
    + int1d(Th1, inside)(
          lambda*v1
    )
    + on(outside, u1=0)
    ;

problem Pb2 (u2, v2, init=i, solver=Cholesky)
    = int2d(Th2)(
          dx(u2)*dx(v2)
        + dy(u2)*dy(v2)
    )
    + int2d(Th2)(
        - v2
    )
    + int1d(Th2, inside)(
        - lambda*v2
    )
    + on(outside, u2=0)
    ;

And, we define a border matrix, because the \(\lambda\) function is none zero inside the domain \(\Omega_1\):

varf b(u2, v2, solver=CG) = int1d(Th1, inside)(u2*v2);
matrix B = b(Vh1, Vh1, solver=CG);

The boundary problem function,

\[\lambda \longrightarrow \int_{\Gamma_i }(u_1-u_2) v_{1}\]

// Boundary problem function
func real[int] BoundaryProblem (real[int] &l){
   lambda[] = l; //make FE function form l
   Pb1;
   Pb2;
   i++; //no refactorization i != 0
   v1 = -(u1-u2);
   lambda[] = B*v1[];
   return lambda[];
}

Note

The difference between the two notations v1 and v1[] is: v1 is the finite element function and v1[] is the vector in the canonical basis of the finite element function v1.

// Solve
real cpu=clock();
LinearCG(BoundaryProblem, p[], eps=1.e-6, nbiter=100);
//compute the final solution, because CG works with increment
BoundaryProblem(p[]); //solve again to have right u1, u2

// Display & Plot
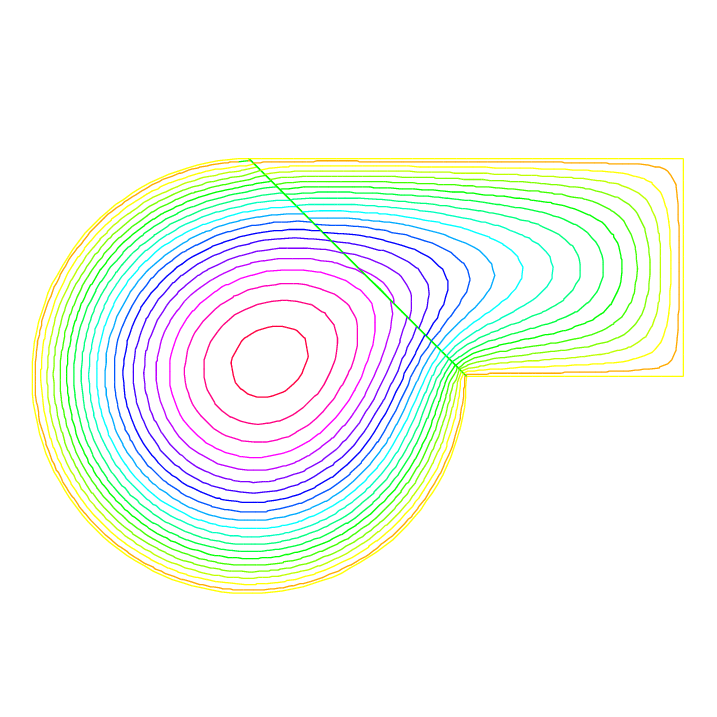
cout << " -- CPU time schwarz-gc:" << clock()-cpu << endl;
plot(u1, u2);