Mesh Generation
Square mesh
1mesh Th0 = square(10 ,10);
2
3mesh Th1 = square(4, 5);
4
5real x0 = 1.2;
6real x1 = 1.8;
7real y0 = 0;
8real y1 = 1;
9int n = 5;
10real m = 20;
11mesh Th2 = square(n, m, [x0+(x1-x0)*x, y0+(y1-y0)*y]);
12
13for (int i = 0; i < 5; ++i){
14 int[int] labs = [11, 12, 13, 14];
15 mesh Th3 = square(3, 3, flags=i, label=labs, region=10);
16 plot(Th3, wait=1, cmm="square flags = "+i );
17}
Mesh adaptation
1// Parameters
2real eps = 0.0001;
3real h = 1;
4real hmin = 0.05;
5func f = 10.0*x^3 + y^3 + h*atan2(eps, sin(5.0*y)-2.0*x);
6
7// Mesh
8mesh Th = square(5, 5, [-1+2*x, -1+2*y]);
9
10// Fespace
11fespace Vh(Th,P1);
12Vh fh = f;
13plot(fh);
14
15// Adaptmesh
16for (int i = 0; i < 2; i++){
17 Th = adaptmesh(Th, fh);
18 fh = f; //old mesh is deleted
19 plot(Th, fh, wait=true);
20}
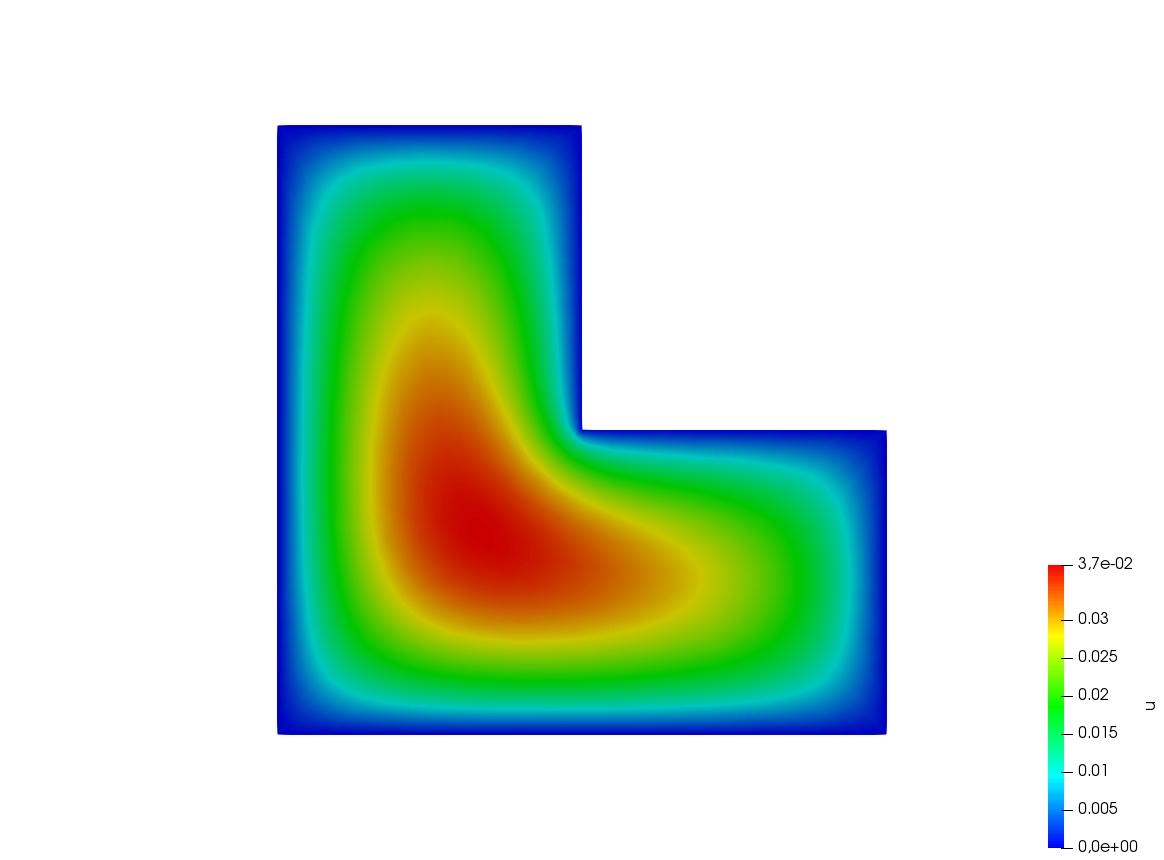
Mesh adaptation for the Poisson’s problem
1// Parameters
2real error = 0.1;
3
4// Mesh
5border ba(t=0, 1){x=t; y=0; label=1;}
6border bb(t=0, 0.5){x=1; y=t; label=1;}
7border bc(t=0, 0.5){x=1-t; y=0.5; label=1;}
8border bd(t=0.5, 1){x=0.5; y=t; label=1;}
9border be(t=0.5, 1){x=1-t; y=1; label=1;}
10border bf(t=0, 1){x=0; y=1-t; label=1;}
11mesh Th = buildmesh(ba(6) + bb(4) + bc(4) + bd(4) + be(4) + bf(6));
12
13// Fespace
14fespace Vh(Th, P1);
15Vh u, v;
16
17// Function
18func f = 1;
19
20// Problem
21problem Poisson(u, v, solver=CG, eps=1.e-6)
22 = int2d(Th)(
23 dx(u)*dx(v)
24 + dy(u)*dy(v)
25 )
26 - int2d(Th)(
27 f*v
28 )
29 + on(1, u=0);
30
31// Adaptmesh loop
32for (int i = 0; i < 4; i++){
33 Poisson;
34 Th = adaptmesh(Th, u, err=error);
35 error = error/2;
36}
37
38// Plot
39plot(u);
Uniform mesh adaptation
1mesh Th = square(2, 2); // The initial mesh
2plot(Th, wait=true);
3
4Th = adaptmesh(Th, 1./30., IsMetric=1, nbvx=10000);
5plot(Th, wait=true);
6
7Th = adaptmesh(Th, 1./30., IsMetric=1, nbvx=10000); // More than one time due to the
8Th = adaptmesh(Th, 1./30., IsMetric=1, nbvx=10000); // adaptation bound `maxsubdiv=`
9plot(Th, wait=true);
Borders
1{
2 int upper = 1;
3 int others = 2;
4 int inner = 3;
5
6 border C01(t=0, 1){x=0; y=-1+t; label=upper;}
7 border C02(t=0, 1){x=1.5-1.5*t; y=-1; label=upper;}
8 border C03(t=0, 1){x=1.5; y=-t; label=upper;}
9 border C04(t=0, 1){x=1+0.5*t; y=0; label=others;}
10 border C05(t=0, 1){x=0.5+0.5*t; y=0; label=others;}
11 border C06(t=0, 1){x=0.5*t; y=0; label=others;}
12 border C11(t=0, 1){x=0.5; y=-0.5*t; label=inner;}
13 border C12(t=0, 1){x=0.5+0.5*t; y=-0.5; label=inner;}
14 border C13(t=0, 1){x=1; y=-0.5+0.5*t; label=inner;}
15
16 int n = 10;
17 plot(C01(-n) + C02(-n) + C03(-n) + C04(-n) + C05(-n)
18 + C06(-n) + C11(n) + C12(n) + C13(n), wait=true);
19
20 mesh Th = buildmesh(C01(-n) + C02(-n) + C03(-n) + C04(-n) + C05(-n)
21 + C06(-n) + C11(n) + C12(n) + C13(n));
22
23 plot(Th, wait=true);
24
25 cout << "Part 1 has region number " << Th(0.75, -0.25).region << endl;
26 cout << "Part 2 has redion number " << Th(0.25, -0.25).region << endl;
27}
28
29{
30 border a(t=0, 2*pi){x=cos(t); y=sin(t); label=1;}
31 border b(t=0, 2*pi){x=0.3+0.3*cos(t); y=0.3*sin(t); label=2;}
32 plot(a(50) + b(30)); //to see a plot of the border mesh
33 mesh Thwithouthole = buildmesh(a(50) + b(30));
34 mesh Thwithhole = buildmesh(a(50) + b(-30));
35 plot(Thwithouthole);
36 plot(Thwithhole);
37}
38
39{
40 real r=1;
41 border a(t=0, 2*pi){x=r*cos(t); y=r*sin(t); label=1;}
42 r=0.3;
43 border b(t=0, 2*pi){x=r*cos(t); y=r*sin(t); label=1;}
44 // mesh Thwithhole = buildmesh(a(50) + b(-30)); // do not do this because the two
45 // circles have the same radius = $0.3$
46}
Change
1verbosity=3;
2
3// Mesh
4mesh Th1 = square(10, 10);
5mesh Th2 = square(20, 10, [x+1, y]);
6
7int[int] r1=[2, 0];
8plot(Th1, wait=true);
9
10Th1 = change(Th1, label=r1); // Change edges' label from 2 to 0
11plot(Th1, wait=true);
12
13int[int] r2=[4, 0];
14Th2 = change(Th2, label=r2); // Change edges' label from 4 to 0
15plot(Th2, wait=true);
16
17mesh Th = Th1 + Th2; // 'gluing together' Th1 and Th2 meshes
18cout << "nb lab = " << int1d(Th1,1,3,4)(1./lenEdge)+int1d(Th2,1,2,3)(1./lenEdge)
19 << " == " << int1d(Th,1,2,3,4)(1./lenEdge) << " == " << ((10+20)+10)*2 << endl;
20plot(Th, wait=true);
21
22fespace Vh(Th, P1);
23Vh u, v;
24
25macro Grad(u) [dx(u),dy(u)] // Definition of a macro
26
27solve P(u, v)
28 = int2d(Th)(
29 Grad(u)'*Grad(v)
30 )
31 -int2d(Th)(
32 v
33 )
34 + on(1, 3, u=0)
35 ;
36
37plot(u, wait=1);

Cube
1load "msh3"
2
3int[int] l6 = [37, 42, 45, 40, 25, 57];
4int r11 = 11;
5mesh3 Th = cube(4, 5, 6, [x*2-1, y*2-1, z*2-1], label=l6, flags =3, region=r11);
6
7cout << "Volume = " << Th.measure << ", border area = " << Th.bordermeasure << endl;
8
9int err = 0;
10for(int i = 0; i < 100; ++i){
11 real s = int2d(Th,i)(1.);
12 real sx = int2d(Th,i)(x);
13 real sy = int2d(Th,i)(y);
14 real sz = int2d(Th,i)(z);
15
16 if(s){
17 int ix = (sx/s+1.5);
18 int iy = (sy/s+1.5);
19 int iz = (sz/s+1.5);
20 int ii = (ix + 4*(iy+1) + 16*(iz+1) );
21 //value of ix,iy,iz => face min 0, face max 2, no face 1
22 cout << "Label = " << i << ", s = " << s << " " << ix << iy << iz << " : " << ii << endl;
23 if( i != ii ) err++;
24 }
25}
26real volr11 = int3d(Th,r11)(1.);
27cout << "Volume region = " << 11 << ": " << volr11 << endl;
28if((volr11 - Th.measure )>1e-8) err++;
29plot(Th, fill=false);
30cout << "Nb err = " << err << endl;
31assert(err==0);

Empty mesh
1{
2 border a(t=0, 2*pi){x=cos(t); y=sin(t); label=1;}
3 mesh Th = buildmesh(a(20));
4 Th = emptymesh(Th);
5 plot(Th);
6}
7{
8 mesh Th = square(10, 10);
9 int[int] ssd(Th.nt);
10 // Builds the pseudo region numbering
11 for(int i = 0; i < ssd.n; i++){
12 int iq = i/2; // Because we have 2 triangles per quad
13 int ix = iq%10;
14 int iy = iq/10;
15 ssd[i] = 1 + (ix>=5) + (iy>=5)*2;
16 }
17 // Builds an emtpy mesh with all edges that satisfy e=T1 cap T2 and ssd[T1] != ssd[T2]
18 Th = emptymesh(Th, ssd);
19 // Plot
20 plot(Th);
21}
3 points
1// Square for Three-Point Bend Specimens fixed on Fix1, Fix2
2// It will be loaded on Load
3real a = 1, b = 5, c = 0.1;
4int n = 5, m = b*n;
5border Left(t=0, 2*a){x=-b; y=a-t;}
6border Bot1(t=0, b/2-c){x=-b+t; y=-a;}
7border Fix1(t=0, 2*c){x=-b/2-c+t; y=-a;}
8border Bot2(t=0, b-2*c){x=-b/2+c+t; y=-a;}
9border Fix2(t=0, 2*c){x=b/2-c+t; y=-a;}
10border Bot3(t=0, b/2-c){x=b/2+c+t; y=-a;}
11border Right(t=0, 2*a){x=b; y=-a+t;}
12border Top1(t=0, b-c){x=b-t; y=a;}
13border Load(t=0, 2*c){x=c-t; y=a;}
14border Top2(t=0, b-c){x=-c-t; y=a;}
15
16mesh Th = buildmesh(Left(n) + Bot1(m/4) + Fix1(5) + Bot2(m/2)
17 + Fix2(5) + Bot3(m/4) + Right(n) + Top1(m/2) + Load(10) + Top2(m/2));
18plot(Th, bw=true);

Bezier
1// A cubic Bezier curve connecting two points with two control points
2func real bzi(real p0, real p1, real q1, real q2, real t){
3 return p0*(1-t)^3 + q1*3*(1-t)^2*t + q2*3*(1-t)*t^2 + p1*t^3;
4}
5
6real[int] p00 = [0, 1], p01 = [0, -1], q00 = [-2, 0.1], q01 = [-2, -0.5];
7real[int] p11 = [1,-0.9], q10 = [0.1, -0.95], q11=[0.5, -1];
8real[int] p21 = [2, 0.7], q20 = [3, -0.4], q21 = [4, 0.5];
9real[int] q30 = [0.5, 1.1], q31 = [1.5, 1.2];
10border G1(t=0, 1){
11 x=bzi(p00[0], p01[0], q00[0], q01[0], t);
12 y=bzi(p00[1], p01[1], q00[1], q01[1], t);
13}
14border G2(t=0, 1){
15 x=bzi(p01[0], p11[0], q10[0], q11[0], t);
16 y=bzi(p01[1], p11[1], q10[1], q11[1], t);
17}
18border G3(t=0, 1){
19 x=bzi(p11[0], p21[0], q20[0], q21[0], t);
20 y=bzi(p11[1], p21[1], q20[1], q21[1], t);
21}
22border G4(t=0, 1){
23 x=bzi(p21[0], p00[0], q30[0], q31[0], t);
24 y=bzi(p21[1], p00[1], q30[1], q31[1], t);
25}
26int m = 5;
27mesh Th = buildmesh(G1(2*m) + G2(m) + G3(3*m) + G4(m));
28plot(Th, bw=true);
Build layer mesh
1load "msh3"
2load "tetgen"
3load "medit"
4
5// Parameters
6int C1 = 99;
7int C2 = 98;
8
9// 2D mesh
10border C01(t=0, pi){x=t; y=0; label=1;}
11border C02(t=0, 2*pi){ x=pi; y=t; label=1;}
12border C03(t=0, pi){ x=pi-t; y=2*pi; label=1;}
13border C04(t=0, 2*pi){ x=0; y=2*pi-t; label=1;}
14
15border C11(t=0, 0.7){x=0.5+t; y=2.5; label=C1;}
16border C12(t=0, 2){x=1.2; y=2.5+t; label=C1;}
17border C13(t=0, 0.7){x=1.2-t; y=4.5; label=C1;}
18border C14(t=0, 2){x=0.5; y=4.5-t; label=C1;}
19
20border C21(t=0, 0.7){x=2.3+t; y=2.5; label=C2;}
21border C22(t=0, 2){x=3; y=2.5+t; label=C2;}
22border C23(t=0, 0.7){x=3-t; y=4.5; label=C2;}
23border C24(t=0, 2){x=2.3; y=4.5-t; label=C2;}
24
25mesh Th = buildmesh(C01(10) + C02(10) + C03(10) + C04(10)
26 + C11(5) + C12(5) + C13(5) + C14(5)
27 + C21(-5) + C22(-5) + C23(-5) + C24(-5));
28
29mesh Ths = buildmesh(C01(10) + C02(10) + C03(10) + C04(10)
30 + C11(5) + C12(5) + C13(5) + C14(5));
31
32// Construction of a box with one hole and two regions
33func zmin = 0.;
34func zmax = 1.;
35int MaxLayer = 10;
36
37func XX = x*cos(y);
38func YY = x*sin(y);
39func ZZ = z;
40
41int[int] r1 = [0, 41], r2 = [98, 98, 99, 99, 1, 56];
42int[int] r3 = [4, 12]; // Change upper surface mesh's triangles labels
43// generated by the 2D mesh's triangles Th
44// from label 4 to label 12
45int[int] r4 = [4, 45]; // Change lower surface mesh's triangles labels
46// generated by the 2D mesh's triangles Th
47// from label 4 to label 45
48
49mesh3 Th3 = buildlayers(Th, MaxLayer, zbound=[zmin, zmax], region=r1,
50 labelmid=r2, labelup=r3, labeldown=r4);
51medit("box 2 regions 1 hole", Th3);
52
53// Construction of a sphere with TetGen
54func XX1 = cos(y)*sin(x);
55func YY1 = sin(y)*sin(x);
56func ZZ1 = cos(x);
57
58real[int] domain = [0., 0., 0., 0, 0.001];
59string test = "paACQ";
60cout << "test = " << test << endl;
61mesh3 Th3sph = tetgtransfo(Ths, transfo=[XX1, YY1, ZZ1],
62 switch=test, nbofregions=1, regionlist=domain);
63medit("sphere 2 regions", Th3sph);
Sphere
1// Parameter
2real hh = 0.1;
3
4// Mesh 2D
5mesh Th = square(10, 20, [x*pi-pi/2, 2*y*pi]); // ]-pi/2, pi/2[X]0, 2pi[
6// A parametrization of a sphere
7func f1 = cos(x)*cos(y);
8func f2 = cos(x)*sin(y);
9func f3 = sin(x);
10// Partial derivative of the parametrization DF
11func f1x = sin(x)*cos(y);
12func f1y = -cos(x)*sin(y);
13func f2x = -sin(x)*sin(y);
14func f2y = cos(x)*cos(y);
15func f3x = cos(x);
16func f3y = 0;
17//M = DF^t DF
18func m11 = f1x^2 + f2x^2 + f3x^2;
19func m21 = f1x*f1y + f2x*f2y + f3x*f3y;
20func m22 = f1y^2 + f2y^2 + f3y^2;
21
22// Periodic condition
23func perio = [[4, y], [2, y], [1, x], [3, x]];
24
25// Mesh adaptation
26real vv = 1/square(hh);
27Th = adaptmesh(Th, m11*vv, m21*vv, m22*vv, IsMetric=1, inquire=1, periodic=perio);
28Th = adaptmesh(Th, m11*vv, m21*vv, m22*vv, IsMetric=1, periodic=perio);
29Th = adaptmesh(Th, m11*vv, m21*vv, m22*vv, IsMetric=1, periodic=perio);
30Th = adaptmesh(Th, m11*vv, m21*vv, m22*vv, IsMetric=1, periodic=perio);
31
32// Sphere
33mesh3 Th3 = movemesh23(Th, transfo=[f1, f2, f3]);
34plot(Th3);