ffddm

class: center, middle, inverse

.title[ffddm]

# Short tutorial

.footnote1[Pierre-Henri Tournier  
Frédéric Nataf  
Pierre Jolivet]

.footnote2[tournier@ljll.math.upmc.fr  
nataf@ljll.math.upmc.fr  
pierre@joliv.et]

---

class: left, top

## [What is **ffddm** ?](../../documentation/ffddm/index.html#ffddm)

- **ffddm** implements a class of parallel solvers in *FreeFEM*:
*overlapping Schwarz domain decomposition methods*

- The entire **ffddm** framework is written in the *FreeFEM* language  
  **ffddm** aims at simplifying the use of parallel solvers in *FreeFEM*  
  You can find the **ffddm** scripts [here](https://github.com/FreeFem/FreeFem-sources/blob/develop/idp) ('ffddm*.idp' files) and examples [here](https://github.com/FreeFem/FreeFem-sources/blob/develop/examples/ffddm)

- **ffddm** provides a set of high-level macros and functions to
  - handle data distribution: distributed meshes and linear algebra
  - build DD preconditioners for your variational problems
  - solve your problem using preconditioned Krylov methods

- **ffddm** implements scalable two level Schwarz methods, with a coarse space correction built
 either from a coarse mesh or a [GenEO](https://link.springer.com/article/10.1007%2Fs00211-013-0576-y#page-1) coarse space  
 *Ongoing research*: approximate coarse solves and three level methods
 
- **ffddm** can also act as a wrapper for the [**HPDDM**](https://github.com/hpddm/hpddm) library  
 **HPDDM** is an efficient C++11 implementation of various domain decomposition methods and Krylov subspace algorithms 
 with advanced block and recycling techniques  
 More details on how to use **HPDDM** within **ffddm** [here](../../documentation/ffddm/documentation.html#using-hpddm-within-ffddm)
 
---

## Why Domain Decomposition Methods ?

How can we solve a large sparse linear system $A u = b \in \mathbb{R}^n$ ?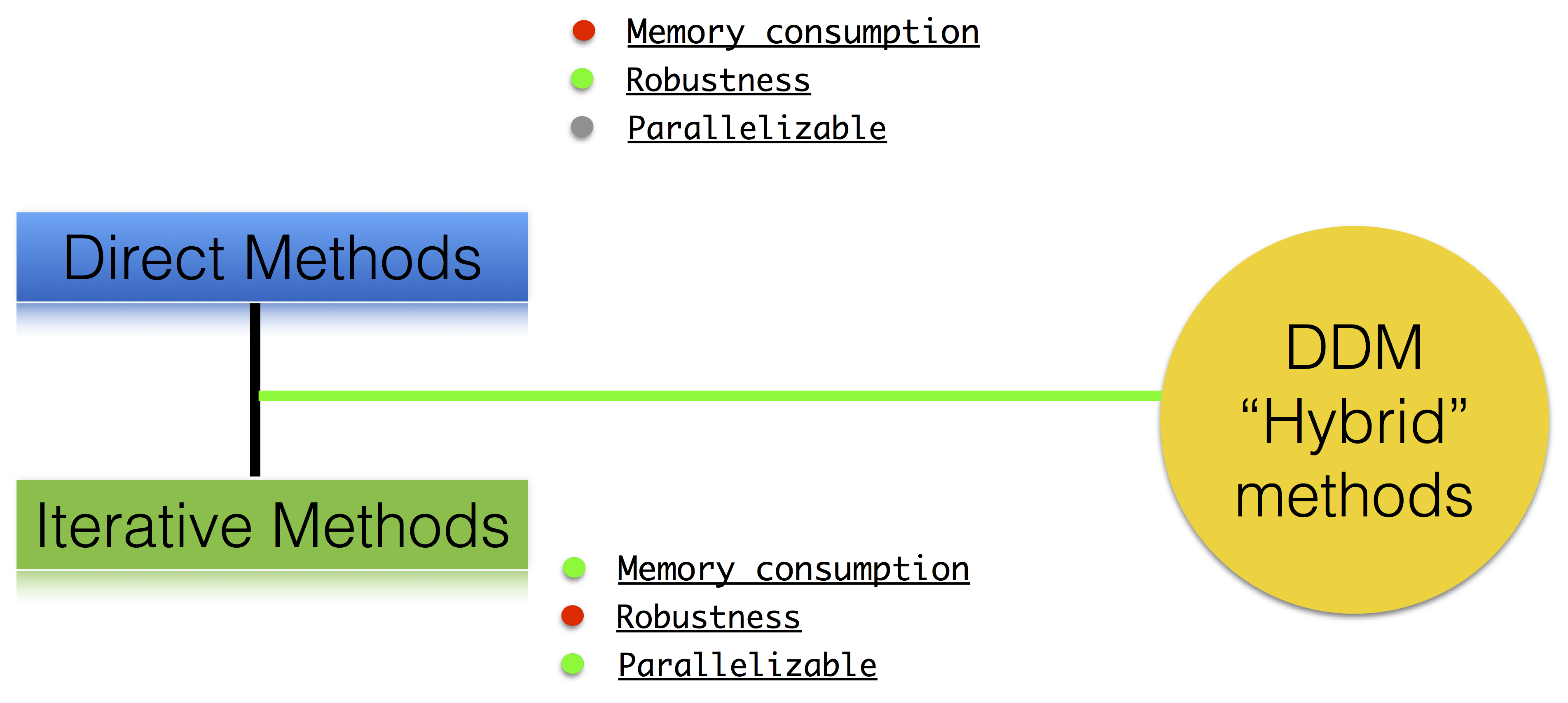

![:scale 100%](../../_images/Methods_Solves_1.png)

---

## [Step 1: Decompose the mesh](../../documentation/ffddm/documentation.html#overlapping-mesh-decomposition)

Build a collection of $N$ overlapping sub-meshes $(Th\_{i})\_{i=1}^N$ from the global mesh $Th$

```cpp
ffddmbuildDmesh( prmesh , ThGlobal , comm )
```

- mesh distributed over the mpi processes of communicator **comm**
- initial mesh **ThGlobal** partitioned with *metis* by default
- size of the overlap given by [ffddmoverlap](../../documentation/ffddm/parameters.html#global-parameters) (default 1)

`prmesh#Thi` is the local mesh of the subdomain for each mpi process

---

```cpp
macro dimension 2// EOM            // 2D or 3D

include "ffddm.idp"

mesh ThGlobal = square(100,100);    // global mesh

*// Step 1: Decompose the mesh
*ffddmbuildDmesh( M , ThGlobal , mpiCommWorld )
```

```cpp
medit("Th"+mpirank, MThi);
```

Copy and paste this to a file 'test.edp' and run it:

```console
$ ff-mpirun -np 2 test.edp -wg
```

---

## [Step 2: Define your finite element](../../documentation/ffddm/documentation.html#local-finite-element-spaces)

```cpp
ffddmbuildDfespace( prfe , prmesh , scalar , def , init , Pk )
```

builds the local finite element spaces and associated distributed operators on top of the mesh decomposition **prmesh**

- **scalar**: type of data for this finite element: *real* or *complex*
- **Pk**: your type of finite element: P1, [P2,P2,P1], ...
- **def**, **init**: macros specifying how to define and initialize a **Pk** FE function

`prfe#Vhi` is the local FE space defined on `prmesh#Thi` for each mpi process

.pull-left[
example for P2 *complex*:
```cpp
macro def(u)  u // EOM
macro init(u) u // EOM
ffddmbuildDfespace( FE, M, complex,
                    def, init, P2 )
```
]
.pull-right[
example for [P2,P2,P1] *real*:
```cpp
macro def(u)  [u, u#B, u#C] // EOM
macro init(u) [u, u, u]     // EOM
ffddmbuildDfespace( FE, M, real, def,
                    init, [P2,P2,P1] )
```
]

---

## [Step 2: Define your finite element](../../documentation/ffddm/documentation.html#local-finite-element-spaces)

### Distributed vectors and restriction operators

Natural decomposition of the set of d.o.f.'s ${\mathcal N}$ of $Vh$ into the $N$ subsets of d.o.f.'s $({\mathcal N}\_i)\_{i=1}^N$ each associated with the local FE space $Vh\_i$

$${\mathcal N} = \cup\_{i=1}^N {\mathcal N}\_i\,, $$
but with duplications of the d.o.f.'s in the overlap

**_Definition_** a *distributed vector* is a collection of local vectors $({\mathbf V\_i})\_{1\le i\le N}$ so that the values on the duplicated d.o.f.'s are the same:

$$
{\mathbf V}\_i = R\_i\,{\mathbf V}, \quad i = 1, ..., N
$$

where ${\mathbf V}$ is the corresponding global vector  
and $R\_i$ is the *restriction operator* from ${\mathcal N}$ into ${\mathcal N}\_i$

**_Remark_** $R\_i^T$ is the *extension operator*: extension by $0$ from ${\mathcal N}\_i$ into ${\mathcal N}$

---

## [Step 2: Define your finite element](../../documentation/ffddm/documentation.html#local-finite-element-spaces)

### Partition of unity

Duplicated unknowns coupled via a *partition of unity*:
$$ I = \sum\_{i = 1}^N R\_i^T D\_i R\_i $$
</div>

$(D\_i)\_{1\le i \le N}$ are square diagonal matrices of size #${\mathcal N}\_i$

$$ {\mathbf V} = \sum\_{i = 1}^N R\_i^T D\_i R\_i {\mathbf V} = \sum\_{i = 1}^N R\_i^T D\_i {\mathbf V\_i} $$

---

## [Step 2: Define your finite element](../../documentation/ffddm/documentation.html#local-finite-element-spaces)

### Data exchange between neighbors

```cpp
func prfe#update(K[int] vi, bool scale)
```

synchronizes local vectors ${\mathbf V}\_i$ between subdomains  
$\Rightarrow$ exchange the values of ${\mathbf V}\_i$ shared with neighbors in the overlap region

$$
  {\mathbf V}\_i \leftarrow R\_i \left( \sum\_{j=1}^N R\_j^T D\_j {\mathbf V}\_j \right) = D\_i {\mathbf V}\_i + \sum\_{j\in \mathcal{O}(i)} R\_i\,R\_j^T\,D\_j {\mathbf V}\_j
 $$
 where $\mathcal{O}(i)$ is the set of neighbors of subdomain $i$. Exchange operators $R_i\,R_j^T$ correspond to neighbor-to-neighbor MPI communications

.pull-left[
 ```cpp
 FEupdate(vi, false);
 ```
 $$
  {\mathbf V}\_i \leftarrow R\_i \left( \sum\_{j=1}^N R\_j^T {\mathbf V}\_j \right)
 $$
 ]
 .pull-right[
 ```cpp
 FEupdate(vi, true);
 ```
 $$
  {\mathbf V}\_i \leftarrow R\_i \left( \sum\_{j=1}^N R\_j^T D\_j {\mathbf V}\_j  \right)
 $$
 ]
---

```cpp
macro dimension 2// EOM            // 2D or 3D

include "ffddm.idp"

mesh ThGlobal = square(100,100);    // global mesh

// Step 1: Decompose the mesh
ffddmbuildDmesh( M , ThGlobal , mpiCommWorld )

*// Step 2: Define your finite element
*macro def(u)  u // EOM
*macro init(u) u // EOM
*ffddmbuildDfespace( FE , M , real , def , init , P2 )
```

```cpp
FEVhi vi = y;
medit("v"+mpirank, MThi, vi);

vi[] = FEDk[mpirank];
medit("D"+mpirank, MThi, vi);

vi = 1;
FEupdate(vi[],true);
ffddmplot(FE,vi,"1")

FEupdate(vi[],false);
ffddmplot(FE,vi,"multiplicity")
```

---

## [Step 3: Define your problem](../../documentation/ffddm/documentation.html#define-the-problem-to-solve)

```cpp
ffddmsetupOperator( pr , prfe , Varf )
```

builds the distributed operator associated to your variational form on top of the distributed FE **prfe**

**Varf** is a macro defining your abstract variational form

```cpp
macro Varf(varfName, meshName, VhName)
    varf varfName(u,v) = int2d(meshName)(grad(u)'* grad(v))
                       + int2d(meshName)(f*v) + on(1, u = 0);  // EOM
```

$\Rightarrow$ assemble local 'Dirichlet' matrices $A\_i = R\_i A R\_i^T$

<div style="overflow: hidden;">
.pull-left31[
$$A = \sum\_{i=1}^N R\_i^T D\_i A\_i R\_i$$
]
.pull-right65[
 **Warning** only true because $D\_i R\_i A = D\_i A\_i R\_i$  
 due to the fact that $D\_i$ vanishes at the interface **!!**
]
</div>

`pr#A` applies $A$ to a distributed vector: ${\mathbf U}\_i \leftarrow R\_i \sum\_{j=1}^N R\_j^T D\_j A\_j {\mathbf V}\_j$

$\Rightarrow$ multiply by $A\_i$ + `prfe#update`

---

```cpp
macro dimension 2// EOM            // 2D or 3D

include "ffddm.idp"

mesh ThGlobal = square(100,100);    // global mesh

// Step 1: Decompose the mesh
ffddmbuildDmesh( M , ThGlobal , mpiCommWorld )

// Step 2: Define your finite element
macro def(u)  u // EOM
macro init(u) u // EOM
ffddmbuildDfespace( FE , M , real , def , init , P2 )

*// Step 3: Define your problem
*macro grad(u) [dx(u), dy(u)] // EOM
*macro Varf(varfName, meshName, VhName)
*    varf varfName(u,v) = int2d(meshName)(grad(u)'* grad(v))
*                       + int2d(meshName)(1*v) + on(1, u = 0);  // EOM
*ffddmsetupOperator( PB , FE , Varf )
*
*FEVhi ui, bi;
*ffddmbuildrhs( PB , Varf , bi[] )
```

```cpp
ui[] = PBA(bi[]);
ffddmplot(FE, ui, "A*b")
```

---

## Summary so far: translating your sequential *FreeFEM* script

<div style="overflow: hidden;">
.pull-left38[
### [Step 1: Decompose the mesh](../../documentation/ffddm/documentation.html#overlapping-mesh-decomposition)
```ff1
mesh Th = square(100,100);
```
]
.pull-right58[

```ff1
mesh Th = square(100,100);
ffddmbuildDmesh(M, Th, mpiCommWorld)
```
]
</div>

<div style="overflow: hidden;">
.pull-left38[
### [Step 2: Define your finite element](../../documentation/ffddm/documentation.html#local-finite-element-spaces)
```ff1
fespace Vh(Th, P1);
```
]
.pull-right58[
```ff1
macro def(u)  u // EOM
macro init(u) u // EOM
ffddmbuildDfespace(FE, M, real, def, init, P1)
```
]
</div>

<div style="overflow: hidden;">
.pull-left38[
### [Step 3: Define your problem](../../documentation/ffddm/documentation.html#define-the-problem-to-solve)
```ff1
varf Pb(u, v) = ...
matrix A = Pb(Vh, Vh);
```
]
.pull-right58[
```ff1
macro Varf(varfName, meshName, VhName)
    varf varfName(u,v) = ... // EOM
ffddmsetupOperator(PB, FE, Varf)
```
]
</div>

---

## [Solve the linear system with the parallel direct solver *MUMPS*](../../documentation/ffddm/documentation.html#define-the-problem-to-solve)

```cpp
func K[int] pr#directsolve(K[int]& bi)
```

We have $A$ and $b$ in distributed form, we can solve the linear system $A u = b$ using the parallel direct solver *MUMPS*

```cpp
// Solve the problem using the direct parallel solver MUMPS
ui[] = PBdirectsolve(bi[]);
ffddmplot(FE, ui, "u")
```

---

## [Step 4: Define the one level DD preconditioner](../../documentation/ffddm/documentation.html#one-level-preconditioners)

```cpp
ffddmsetupPrecond( pr , VarfPrec )
```

builds the one level preconditioner for problem **pr**.

By default it is the *Restricted Additive Schwarz (RAS)* preconditioner:

$$
M^{-1}\_1 = M^{-1}\_{\text{RAS}} = \sum\_{i=1}^N R\_i^T D\_i A\_i^{-1} R\_i \quad \text{with}\; A\_i = R\_i A R\_i^T
$$

**_Setup step_**: compute the $LU$ (or $L D L^T$) factorization of local matrices $A\_i$

`pr#PREC1` applies $M^{-1}\_1$ to a distributed vector: ${\mathbf U}\_i \leftarrow R\_i \sum\_{j=1}^N R\_j^T D\_j A\_j^{-1} {\mathbf V}\_i$

$\Rightarrow$ apply $A\_i^{-1}$ (forward/backward substitutions) + `prfe#update`

---

## [Step 5: Solve the linear system with preconditioned GMRES](../../documentation/ffddm/documentation.html#solving-the-linear-system)

```cpp
func K[int] pr#fGMRES(K[int]& x0i, K[int]& bi, real eps, int itmax, string sp)
```

solves the linear system with flexible GMRES with DD preconditioner $M^{-1}$

- **x0i**: initial guess
- **bi**: right-hand side
- **eps**: relative tolerance
- **itmax**: maximum number of iterations
- **sp**: `"left"` or `"right"` preconditioning

.pull-left[
.center[*left preconditioning*]

.center[solve $M^{-1} A x = M^{-1} b$]
]
.pull-right[
.center[*right preconditioning*]

.center[solve $A M^{-1} y = b$]
.center[$\Rightarrow x = M^{-1} y$]
]

---

```cpp
macro dimension 2// EOM            // 2D or 3D
include "ffddm.idp"

mesh ThGlobal = square(100,100);    // global mesh
// Step 1: Decompose the mesh
ffddmbuildDmesh( M , ThGlobal , mpiCommWorld )
// Step 2: Define your finite element
macro def(u)  u // EOM
macro init(u) u // EOM
ffddmbuildDfespace( FE , M , real , def , init , P2 )
// Step 3: Define your problem
macro grad(u) [dx(u), dy(u)] // EOM
macro Varf(varfName, meshName, VhName)
    varf varfName(u,v) = int2d(meshName)(grad(u)'* grad(v))
                       + int2d(meshName)(1*v) + on(1, u = 0);  // EOM
ffddmsetupOperator( PB , FE , Varf )

FEVhi ui, bi;
ffddmbuildrhs( PB , Varf , bi[] )

*// Step 4: Define the one level DD preconditioner
*ffddmsetupPrecond( PB , Varf )

*// Step 5: Solve the linear system with GMRES
*FEVhi x0i = 0;
*ui[] = PBfGMRES(x0i[], bi[], 1.e-6, 200, "right");
```

```cpp
ffddmplot(FE, ui, "u")
PBwritesummary
```

---

## [Define a two level DD preconditioner](../../documentation/ffddm/documentation.html#two-level-preconditioners)

**Goal** improve scalability of the one level method

$\Rightarrow$ enrich the one level preconditioner with a *coarse problem* coupling all subdomains

Main ingredient is a rectangular matrix $\color{red}{Z}$ of size $n \times n\_c,\,$ where $n\_c \ll n$  
$\color{red}{Z}$ is the *coarse space* matrix

The *coarse space operator* $E = \color{red}{Z}^T A \color{red}{Z}$ is a square matrix of size $n\_c \times n\_c$

The simplest way to enrich the one level preconditioner is through the *additive coarse correction* formula:

$$M^{-1}\_2 = M^{-1}\_1 + \color{red}{Z} E^{-1} \color{red}{Z}^T$$

.center[*How to choose $\color{red}{Z}$ ?*]

---

## [Build the GenEO coarse space](../../documentation/ffddm/documentation.html#building-the-geneo-coarse-space)

```cpp
ffddmgeneosetup( pr , Varf )
```

The *GenEO* method builds a robust coarse space for highly heterogeneous or anisotropic **SPD** problems

$\Rightarrow$ solve a local generalized eigenvalue problem in each subdomain

$$
D\_i A\_i D\_i\, V\_{i,k} = \lambda\_{i,k}\, A\_i^{\text{Neu}} \,V\_{i,k}
$$

with $A\_i^{\text{Neu}}$ the local Neumann matrices built from **Varf** (same **Varf** as [Step 3](tutorial-slides.html#11))

The GenEO coarse space is $\color{red}{Z} = (R\_i^T D\_i V\_{i,k})^{i=1,...,N}\_{\lambda\_{i,k} \ge \color{blue}{\tau}}$  
The eigenvectors $V\_{i,k}$ selected to enter the coarse space correspond to eigenvalues $\lambda_{i,k} \ge \color{blue}{\tau}$, where $\color{blue}{\tau}$ is a threshold parameter 
 
 **Theorem**   
 the spectrum of the preconditioned operator lies in the interval $[\displaystyle \frac{1}{1+k_1 \color{blue}{\tau}} , k_0 ]$  
 where $k_0 - 1$ is the \# of neighbors and $k_1$ is the multiplicity of intersections  
 $\Rightarrow$ $k_0$ and $k_1$ do not depend on $N$ nor on the PDE

---

```cpp
macro dimension 2// EOM            // 2D or 3D
include "ffddm.idp"

FEVhi ui, bi;
ffddmbuildrhs( PB , Varf , bi[] )

// Step 4: Define the one level DD preconditioner
ffddmsetupPrecond( PB , Varf )

*// Build the GenEO coarse space
*ffddmgeneosetup( PB , Varf )

// Step 5: Solve the linear system with GMRES
FEVhi x0i = 0;
ui[] = PBfGMRES(x0i[], bi[], 1.e-6, 200, "right");
```

---

## [Build the coarse space from a coarse mesh](../../documentation/ffddm/documentation.html#building-the-coarse-space-from-a-coarse-mesh)

```cpp
ffddmcoarsemeshsetup( pr , Thc , VarfEprec , VarfAprec )
```

For **non SPD** problems, an alternative is to build the coarse space by discretizing the PDE on a coarser mesh **Thc**

.red[$Z$] will be the *interpolation matrix* from the coarse FE space ${Vh}\_c$ to the original FE space $Vh$

$\Rightarrow E=\color{red}{Z}^{T} A \color{red}{Z}$ is the matrix of the problem discretized on the coarse mesh

The variational problem to be discretized on **Thc** is given by macro **VarfEprec**

**VarfEprec** can differ from the original **Varf** of the problem  
        *Example*: added absorption for wave propagation problems
  
Similarly, **VarfAprec** specifies the global operator involved in multiplicative coarse correction formulas. It defaults to $A$ if **VarfAprec** is not defined

---

```cpp
macro dimension 2// EOM            // 2D or 3D
include "ffddm.idp"

FEVhi ui, bi;
ffddmbuildrhs( PB , Varf , bi[] )

// Step 4: Define the one level DD preconditioner
ffddmsetupPrecond( PB , Varf )

*// Build the coarse space from a coarse mesh
*mesh Thc = square(10,10);
*ffddmcoarsemeshsetup( PB , Thc , Varf , null )

// Step 5: Solve the linear system with GMRES
FEVhi x0i = 0;
ui[] = PBfGMRES(x0i[], bi[], 1.e-6, 200, "right");
```

---

## [Use **HPDDM** within **ffddm**](../../documentation/ffddm/documentation.html#using-hpddm-within-ffddm)

**ffddm** allows you to use **HPDDM** to solve your problem,
effectively replacing the **ffddm** implementation of all parallel linear algebra computations

$\Rightarrow$ define your problem with **ffddm**, solve it with **HPDDM**  
$\Rightarrow$ **ffddm** acts as a finite element interface for **HPDDM**

You can use **HPDDM** features unavailable in **ffddm** such as advanced Krylov subspace methods
implementing block and recycling techniques

To switch to **HPDDM**, simply define the macro `pr#withhpddm` before using `ffddmsetupOperator` ([Step 3](tutorial-slides.html#11)). You can then pass **HPDDM** options
with command-line arguments or directly to the underlying **HPDDM** operator. Options need to be prefixed by the operator prefix:

```cpp
macro PBwithhpddm()1 // EOM
ffddmsetupOperator( PB , FE , Varf )
set(PBhpddmOP,sparams="-hpddm_PB_krylov_method gcrodr -hpddm_PB_recycle 10");
```

Or, define `pr#withhpddmkrylov` to use **HPDDM** only for the Krylov method

Example [here](https://github.com/FreeFem/FreeFem-sources/blob/develop/examples/ffddm/Helmholtz-2d-HPDDM-BGMRES.edp): Helmholtz problem with multiple rhs solved with Block GMRES

---

## Some results: Heterogeneous 3D elasticity with GenEO

Heterogeneous 3D linear elasticity equation discretized with P2 FE  
solved on 4096 MPI processes  
$n\approx$ 262 million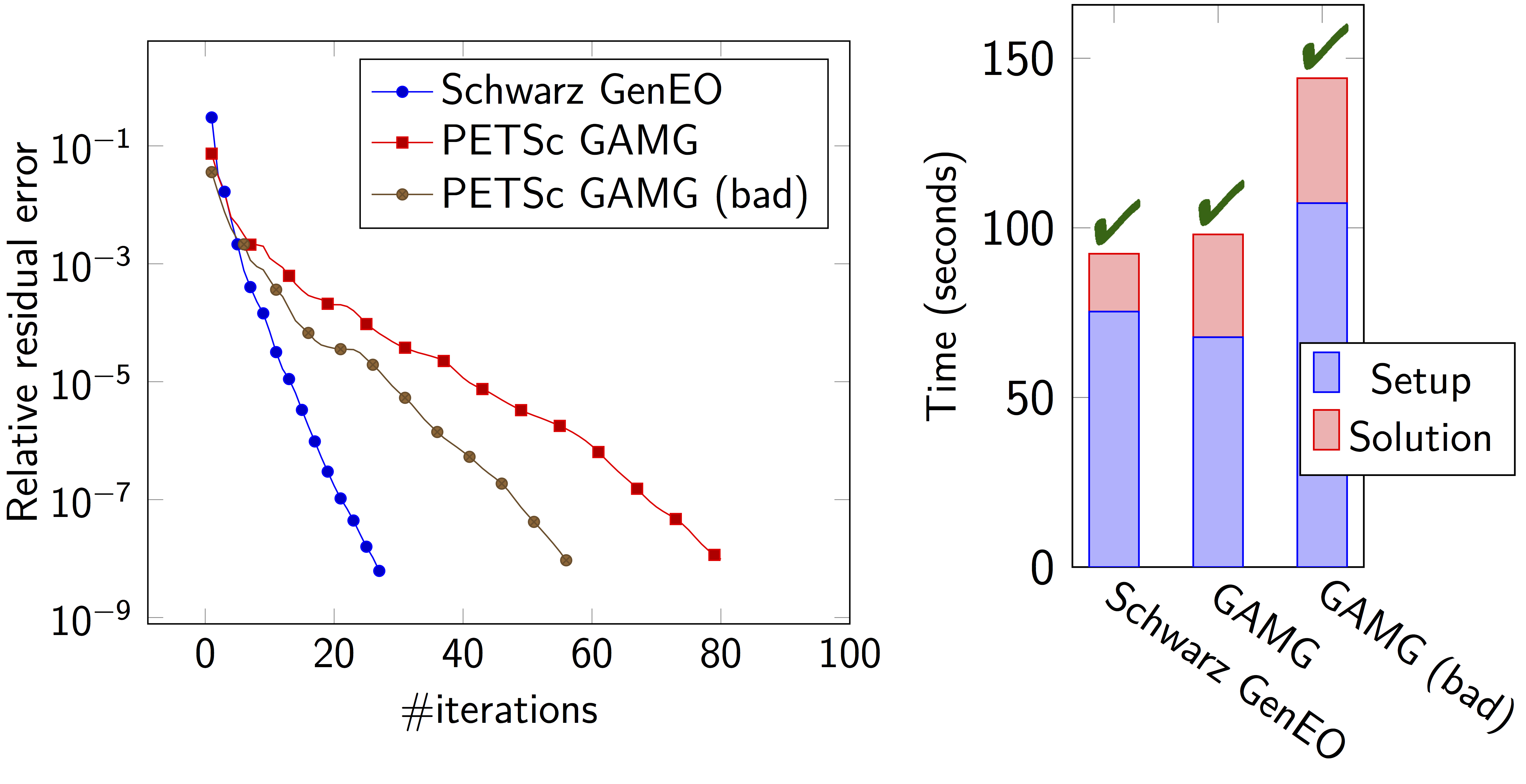

![:scale 100%](../../_images/comparisonAMG.png)

---

## Some results: 2-level DD for Maxwell equations, scattering from the COBRA cavity

---

## Some results: 2-level DD for Maxwell equations, scattering from the COBRA cavity

- order 2 Nedelec edge FE
- fine mesh: 10 points per wavelength
- coarse mesh: 3.33 points per wavelength
- two level ORAS preconditioner with added absorption
- f = 10 GHz: $n\approx$ 107 million, .red[$n_c \approx$ 4 million]  
f = 16 GHz: $n\approx$ 198 million, .red[$n_c \approx$ 7.4 million]

$\rightarrow$ coarse problem too large for a direct solver  
$\Rightarrow$ inexact coarse solve: GMRES + one level ORAS preconditioner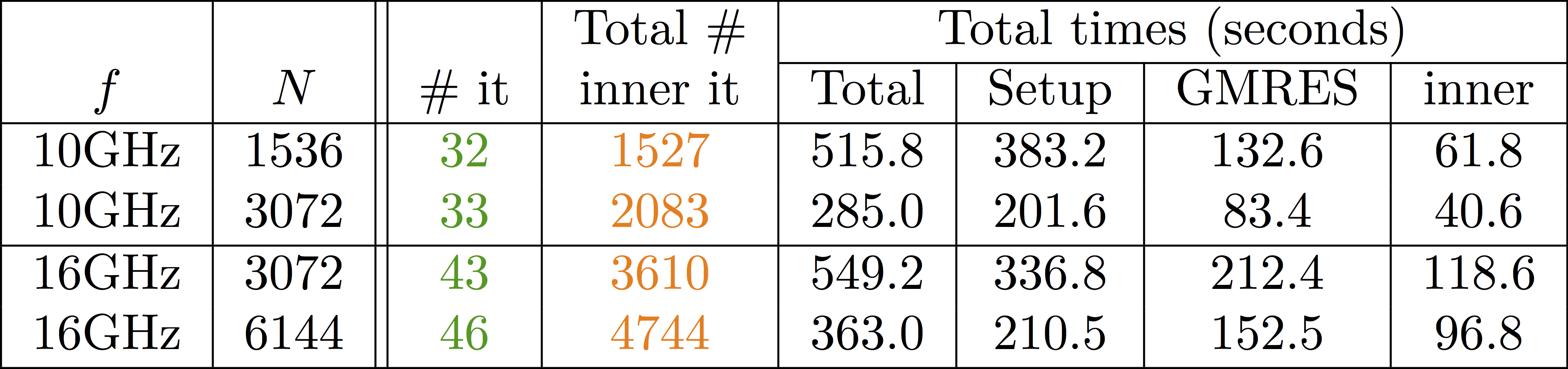

![:scale 100%](../../_images/table.png)

speedup of 1.81 from 1536 to 3072 cores at 10GHz  
                     1.51 from 3072 to 6144 cores at 16GHz

You can find the script [here](https://github.com/FreeFem/FreeFem-sources/blob/develop/examples/ffddm/Maxwell_Cobracavity.edp)